Chuletas y apuntes de Matemáticas de Bachillerato y Selectividad

1. Bizitzaren Hasiera eta Lehen Hominidoak

Sistema Sexagesimal

Conversión de grados, minutos y segundos.

Conversión de Complejos a Incomplejos (Grados a Minutos/Segundos)

• Minutos (x'): Multiplicar los grados (#°) por 60. Fórmula: x' = #° * (60') / 1°
• Segundos (x"): Multiplicar los minutos (#') por 60. Fórmula: x" = #' * (60") / 1'

Conversión de Incomplejos a Complejos (Segundos/Minutos a Grados)

• Minutos desde Segundos (x'): Dividir los segundos (#") entre 60. Fórmula: x' = #" * (1') / 60"
• Grados desde Minutos (x°): Dividir los minutos (#') entre 60. Fórmula: x° = #' * (1°) / 60'

Sistema Circular

Relación entre grados sexagesimales y radianes.

• Grados a Radianes: Multiplicar los grados (#°) por π y dividir entre 180°. Fórmula: Radianes = #° * (π rad) / 180°
• Radianes a Grados:

Defina los conceptos de ángulo de dos vectores no nulos y de vectores ortogonales en R^n

Definición

Dado dos vectores no nulos x,y€R^n se define eñ ángulo formado por x e y como el único numero Φ€[0,Pi tal que el cosΦ=(x|y)/||x|| ||y||

Se dice que dos vectores x,y€Rⁿ son ortogonales si (x|y)=0. Si A wa un subconjunto no vacío de Rⁿ se llama complemento ortogonal de A al conjunto

A™ = { x€Rⁿ  (x|a) =0 √a€A}

Si x,y€Rⁿ son vectores no nulos, se llama proyección ortogona de x sobre y al vector ηy(x)=((x|y/(y|y) y

Defina los conjuntos bola abierta, bola cerrada y esfera en R^n. (con una norma arbitraria ||.||)

Sea ||.|| una norma arbitraria en R^n. Sean a€R^n y r€R^+. La bola abierta en R^n de centro a y de radio r es el... Continuar leyendo "Ángulos entre Vectores, Conjuntos Abiertos y Cerrados en R^n" »

Conceptos Fundamentales de Convexidad y Cálculo Diferencial

Conjuntos Convexos

• Un conjunto definido por una restricción lineal de igualdad (=) es convexo (hiperplano).
  Ejemplo: S = {(X,Y) | 2X - 3Y = 4}
• Un conjunto definido por una restricción lineal de desigualdad (< o >) es convexo (semiespacio).
• El conjunto de puntos donde una función estrictamente convexa es mayor que una constante ({x | f(x) > c}) es convexo.
• El conjunto de puntos donde una función estrictamente cóncava es menor que una constante ({x | f(x) < c}) es convexo.
• La intersección de conjuntos convexos es convexa.

Funciones y Convexidad

• Una función f(x) es convexa si su matriz Hessiana (Hf) es semidefinida positiva (SDP).
• Una función f(x) es cóncava si su matriz

Continuidad de una Función

-Función continua: Una función f es continua en un punto x=a de su dominio si lim f(x) (cuando x tiende a a) = f(a). Esto implica que existe el límite de la función en el punto x=a, f está definida en x=a, existe f(a), y ambos valores son iguales.

Tipos de Discontinuidad

1. Discontinuidad evitable: Existe el límite pero no coincide con f(a). lim f(x) (cuando x tiende a a) ≠ f(a)
2. Discontinuidad de 1ª especie o de salto: Existen los límites laterales pero no son iguales. L1 = lim f(x) (cuando x tiende a a +) ≠ lim f(x) (cuando x tiende a a -) = L2.
3. Discontinuidad de 2ª especie: Cuando alguno (o ambos) de los límites laterales no existen.

Asíntotas

AH: lim f(x) (cuando x tiende a +-inf) = nº.

AV: lim f(x) (cuando... Continuar leyendo "Continuidad, Derivadas y Matrices: Conceptos Clave en Matemáticas" »

Conceptos Clave de Geometría Analítica

La Recta

Pendiente (m): La pendiente de una recta se relaciona con el ángulo de inclinación (θ) respecto al eje x positivo.

m = tgθ

Condiciones de Paralelismo y Perpendicularidad

• Para que dos rectas sean paralelas:

  m₁ = m₂

• Para que dos rectas sean perpendiculares:

  m₁ * m₂ = -1

  

Comprobaciones Geométricas mediante Pendientes

• Comprobación de triángulo rectángulo: Dos pendientes de los lados deben ser recíprocas y de signo contrario (es decir, su producto debe ser -1).

  Ejemplo: y

• Comprobación de un paralelogramo: Se calculan las 4 pendientes de los lados. Si los lados opuestos tienen pendientes iguales, es un paralelogramo.

  Ejemplo: m₁ = m₄ y m₃ = m₂

Ángulo entre Dos Rectas

La tangente del... Continuar leyendo "Fórmulas Esenciales de Rectas, Circunferencias y Parábolas" »

Designación de Datos y Frecuencias

Designación de los datos estadísticos

En un estudio estadístico bidimensional, los datos se recogen por parejas, ya que se estudian 2 características, y los signos escritos que se utilizan para referirse a cada pareja son x_i, y_i.

Frecuencia absoluta

La frecuencia absoluta de una pareja es el número de veces que se repite.

Designación de las frecuencias absolutas

El signo escrito que se utiliza para referirse a la frecuencia absoluta de la pareja x_i, y_i es f_i.

Medidas de Relación Lineal

Covarianza

Se designa por σ_xy y se define por la siguiente fórmula:

σ_xy =

Coeficiente de correlación lineal

Se designa por r y se define por la siguiente fórmula en la que σ_x es la desviación típica de los datos designados... Continuar leyendo "Estadística Bidimensional: Conceptos Fundamentales y Cálculo Práctico" »

Trazado de Circunferencias Tangentes: Métodos y Casos Prácticos

A continuación, se detallan diversos métodos para la construcción de circunferencias tangentes, abordando diferentes configuraciones de elementos dados (puntos, rectas y otras circunferencias). Cada sección describe un caso específico con sus pasos de construcción.

Circunferencia Tangente a un Punto (T), una Recta (r) y una Circunferencia (c)

(Caso Pc(T), r, c)

1. Unir el centro de la circunferencia dada (C) con el punto T.
2. Unir el punto T con un punto P (punto de tangencia en la recta) y trazar su mediatriz.
3. El centro buscado (O) se halla en la intersección de la mediatriz con la línea C-T.

Circunferencia Tangente a un Punto (T) en una Recta (r) y a otra Circunferencia (c)

(Caso

Continuidad

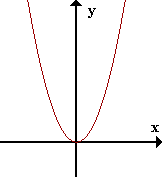\(f(x) = x^2\)

Intuitivamente, la continuidad significa que un pequeño cambio en la variable \(x\) implica sólo un pequeño cambio en el valor de \(f(x)\), es decir, la gráfica consiste de un sólo trozo de curva.

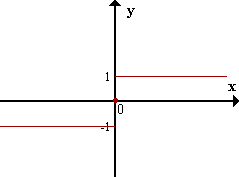\(f(x) = \text{sgn} \, x\)

En contraste, una gráfica como la de la función \(f(x) = \text{sgn} \, x\) (signo de \(x\)) que consiste de pedazos de curva separados por un vacío en una abscisa exhibe allí una discontinuidad.

La continuidad de la función \(f(x)\) para un valor \(a\) significa que \(f(x)\) difiere arbitrariamente poco del valor \(f(a)\) cuando \(x\) está suficientemente cerca de \(a\).

Expresemos esto en términos del concepto de límite...

Definición

Continuidad

Una función \(f(x)\) es continua en un punto... Continuar leyendo "Funciones Continuas y Discontinuas: Definiciones y Ejemplos" »