Conceptos Esenciales de Probabilidad y Estadística: Teoremas y Métodos Fundamentales
Enviado por Programa Chuletas y clasificado en Matemáticas
Escrito el en  español con un tamaño de 8,71 KB
español con un tamaño de 8,71 KB
Conceptos Fundamentales en Probabilidad y Estadística
Este documento explora definiciones y teoremas esenciales que constituyen la base de la probabilidad y la estadística, herramientas indispensables para el análisis de datos y la toma de decisiones.
Teoremas Clave en Probabilidad
Ley de los Grandes Números
La Ley de los Grandes Números es un teorema fundamental en probabilidad que describe el comportamiento del promedio de una sucesión de variables aleatorias a medida que el número total de variables aumenta. Este teorema establece las condiciones bajo las cuales dicho promedio converge (en los sentidos que se explicarán más adelante) al promedio de las esperanzas de las variables aleatorias involucradas.
Teorema de Chebyshev
El Teorema
... Continuar leyendo "Conceptos Esenciales de Probabilidad y Estadística: Teoremas y Métodos Fundamentales" »
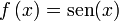

















 gallego con un tamaño de 1,04 KB
gallego con un tamaño de 1,04 KB