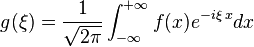Transformada de Fourier (TF)

Enviado por Anónimo y clasificado en Matemáticas

Escrito el 28 de Enero de 2008 en español con un tamaño de 14,05 KB

En matematica, la transformada de Fourier es una aplicación que hace corresponder a una función f con valores reales o complejos y definida en la recta, otra función g definida de la manera siguiente:

$g(\\\\\\\\xi ) = \\\\\\\\frac{1}\\\\\\\\sqrt{2\\\\\\\\pi} \\\\\\\\int_{-\\\\\\\\infty}^{+\\\\\\\\infty} f(x)e^{-i\\\\\\\\xi\\\\\\\\,x} dx$

Donde f es $L 1$ , o sea f tiene que ser una función integrable en el sentido de la integral de Lebesgue. El factor que acompaña la integral en definición facilita el enunciado de algunos de los teoremas referentes a la transformada de Fourier. Aunque esta forma de normalizar la transformada de Fourier es la más comúnmente adoptada, no es universal.

La transformada de Fourier así definida goza de una serie de propiedades de continuidad que garantizan que puede extenderse a espacios de funciones mayores e incluso a espacios de funciones generalizadas.

La transformada de Fourier tiene una multitud de aplicaciones en muchas áreas de la ciencia e ingeniería: la física, la teoría de los números, la combinatoria, el procesamiento de señales, la teoría de la probabilidad, la estadística, la óptica, la propagación de ondas y otras áreas. En procesamiento de señales la transformada de Fourier suele considerarse como la decomposición de una señal en componentes de frecuencias diferentes, es decir, g corresponde al espectro de frecuencias de la señal f.

La rama de la matemática que estudia la transformada de Fourier y sus generalizaciones es denominada análisis armónico.

Son varias las notaciones que se utilizan para la transformada de Fourier de f. Hé aquí algunas de ellas: $\\\\\\\\mathcal{F}[f], \\\\\\\\hat f, F(f)$ .

Definición formal

Sea f una función Lebesgue integrable:

$f \\\\\\\\in L^1(\\\\\\\\mathbb{R})$ o $f \\\\\\\\in L^1(\\\\\\\\mathbb{C})$

La transformada de Fourier de f es la función

$\\\\\\\\hat{f}(\\\\\\\\xi ) = \\\\\\\\frac{1}\\\\\\\\sqrt{2\\\\\\\\pi} \\\\\\\\int_{-\\\\\\\\infty}^{+\\\\\\\\infty} f(x)e^{-i\\\\\\\\xi\\\\\\\\,x} dx$

Esta integral tiene sentido, pues el integrando es una función integrable. Una estimativa simple demuestra que la transformada de Fourier F(f) es una función acotada. Además por medio del teorema de convergencia dominada puede demostrarse que F(f) es continua.

La transformada de Fourier inversa de una función integrable f está definida por:

$\\\\\\\\check{f}(\\\\\\\\xi ) = \\\\\\\\frac{1}\\\\\\\\sqrt{2\\\\\\\\pi} \\\\\\\\int_{-\\\\\\\\infty}^{+\\\\\\\\infty} f(x)e^{i\\\\\\\\xi\\\\\\\\,x} dx$

Nótese que la única diferencia entre la transformada de Fourier y la transformada de Fourier inversa es el signo negativo en el exponente del integrando. El teorema de inversión de Fourier formulado abajo justifica el nombre de transformada de Fourier inversa dado a esta transformada.

Propiedades básicas

La transformada de Fourier es una aplicación lineal:

$\\\\\\\\mathcal{F}[a\\\\\\\\cdot f+b \\\\\\\\cdot g]=a\\\\\\\\mathcal{F}[f]+b\\\\\\\\mathcal{F}[g].$

Valen las siguientes propiedades para una función absolutamente integrable f:

Cambio de escala:

$\\\\\\\\mathcal{F} [t \\\\\\\\mapsto f(at)](\\\\\\\\omega) = \\\\\\\\frac{1}{|a|} \\\\\\\\mathcal{F}[f]\\\\\\\\bigg(\\\\\\\\frac{\\\\\\\\omega}{a}\\\\\\\\bigg)$

Traslación:

$\\\\\\\\mathcal{F}[t \\\\\\\\mapsto f(t-a)](\\\\\\\\omega)=e^{-i\\\\\\\\omega a} \\\\\\\\mathcal{F}[f](\\\\\\\\omega)$

Traslación en la variable transformada:

$[\\\\\\\\mathcal{F}(f)](\\\\\\\\omega-a)= \\\\\\\\mathcal{F}[t \\\\\\\\mapsto e^{iat} f(t)](\\\\\\\\omega)$

Transformada de la derivada: Si f y su derivada son integrables,

$\\\\\\\\mathcal F [f'](\\\\\\\\omega) = i\\\\\\\\omega \\\\\\\\hat f(\\\\\\\\omega)$

Derivada de la transformada: Si f y t ? f(t) son integrables, la transformada de Fourier F(f) es diferenciable

$\\\\\\\\mathcal{F}(f)' (\\\\\\\\omega) = \\\\\\\\mathcal{F} [t \\\\\\\\mapsto (-it)f(t)](\\\\\\\\omega)$

Estas identidades se demuestran por una mudanza de variables o integración por partes.

En lo que sigue, definimos la convolución de dos funciones f, g en la recta se define da la manera siguiente:

$[f \\\\\\\\star g](x) = \\\\\\\\frac{1}{\\\\\\\\sqrt{2 \\\\\\\\pi}} \\\\\\\\int_{-\\\\\\\\infty}^{+\\\\\\\\infty} f(y) g(x - y) dy.$

Nuevamente la presencia del factor delante de la integral simplifica el enunciado de los resultados como el que sigue: Si f y g son funciones absolutamente integrables, la convolución también es integrable, y vale la igualdad:

$\\\\\\\\mathcal{F}[f*g] = \\\\\\\\mathcal{F}[f] \\\\\\\\cdot \\\\\\\\mathcal{F}[g]$

También puede enunciarse un teorema análogo para la convolución en la variable transformada,

$\\\\\\\\mathcal{F}[f \\\\\\\\cdot g] =\\\\\\\\mathcal{F}[f]*\\\\\\\\mathcal{F}[g].$

pero este exige cierto cuidado con el dominio de definición de la transformada de Fourier.

Tabla de Transformadas básicas

En algunas ocasiones se define la transformada con un factor multiplicativo diferente de $\\\\\\\\frac{1}\\\\\\\\sqrt{2\\\\\\\\pi}$ , siendo frecuente en ingeniería el uso de un factor unidad en la transformada directa y un factor de $\\\\\\\\frac{1}{2\\\\\\\\pi}$ en la transformada inversa. A continuación se lista una tabla de funciones y sus transformadas de Fourier con un factor unidad. Si uno desea utilizar otro factor, sólo debe multiplicar la segunda columna por ese factor.

Función	Transformada
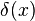$\\\\\\\\delta(x) \\\\\\\\!$	$1 \\\\\\\\!$
$u(x) \\\\\\\\!$	$1/2(\\\\\\\\delta(f)+1/(j\\\\\\\\pi f)) \\\\\\\\!$
$sin(w_0 x) \\\\\\\\!$	$-i\\\\\\\\pi[\\\\\\\\delta(w-w_0)-\\\\\\\\delta(w+w_0)] \\\\\\\\!$
$cos(w_0 x) \\\\\\\\!$	$\\\\\\\\pi[\\\\\\\\delta(w-w_0)+\\\\\\\\delta(w+w_0)] \\\\\\\\!$

Teorema de inversión

La idea del teorema de inversión es que dado una función f, la transformada de Fourier inversa aplicada a la transformada de Fourier de f resulta en la función original, en símbolos:

$(1) \\\\\\\\quad \\\\\\\\check{\\\\\\\\hat{f}} = f \\\\\\\\quad$

Sin embargo, el resultado formulado de esta forma no es válido, porque el dominio de la transformada de Fourier como lo hemos definido en el primer párrafo de este artículo no es invariante, o sea que la transformada de Fourier de una función integrable no es necesariamente integrable.

Para formular el teorema de inversión necesitamos encontrar espacios de funciones que sean invariantes bajo la transformada de Fourier. De hecho, hay numerosas posibilidades, la más natural del punto de vista técnico siendo el espacio de Schwartz de funciones ? rápidamente decrecientes. Sin embargo aquí tomamos un camino más directo para formular un enunciado:

Teorema. El espacio de funciones complejas f definidas en la recta tales que f y la transformada de Fourier de f sean integrables, es invariante tanto por la transformada de Fourier que por la transformada de Fourier inversa. Además para una función f en este espacio, vale el teorema de inversión (1).

Otra posibilidad para formular un teorema de inversión se fundamenta en el hecho de que la transformada de Fourier tiene muchas extensiones naturales.

Uso en ingeniería

La transformada de Fourier se utiliza para pasar al «dominio de la frecuencia» una señal para así obtener información que no es evidente en el dominio del tiempo. Se demuestra matemáticamente que una señal periódica se puede descomponer en una suma de senos y cosenos formando una base ortogonal, de esta forma, señales como la voz o las ondas se pueden descomponer en un sumitario de señales trigonometricas. El conjunto de constantes que multiplican a cada frecuencia forman el espectro de frecuencias. De esta forma se pueden llegar a diversos experimentos muy interesantes:

1- La voz humana recorre el espectro de los 300Hz a los 3400Hz. 2- Si conocemos la densidad espectral de un sistema y la entrada podemos conocer la densidad espectral de la salida. Esto es muy útil para el diseño de filtros de radiotransistores.

Transformada rápida de Fourier

FFT es la abreviatura usual (del inglés Fast Fourier Transform) de un eficiente algoritmo que permite calcular la transformada de Fourier discreta (DFT) y su inversa. La FFT es de gran importancia en una amplia variedad de aplicaciones, desde el tratamiento digital de señales y filtrado digital en general a la resolución de ecuaciones diferenciales parciales o los algoritmos de multiplicación rápida de grandes enteros.

Aplicaciones

MP3
Reducción de ruido en señales, como el ruido blanco
Análisis en frecuencia de cualquier señal discreta.
Tratamiento de imagen (JPEG)) y audio
Análisis de materiales y estadística
Síntesis, mediante la transformada inversa IFFT

Entradas relacionadas:

Etiquetas: