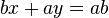Ecuaciones de la recta
Enviado por Programa Chuletas y clasificado en Matemáticas
Escrito el en  español con un tamaño de 5,37 KB
español con un tamaño de 5,37 KB
Ecuación de la recta
Se puede obtener la ecuación de la recta a partir de la fórmula de la pendiente:
 |
Esta forma de obtener la ecuación de una recta se suele utilizarcuando se conocen su pendiente y las coordenadas de uno de sus puntos.La pendiente m es la tangente de la recta con el eje de abscisas.
Forma simplificada de la ecuación de la recta
Si se conocen la pendiente y la ordenada del punto donde la recta secorta con el eje de las ordenadas, se sustituye en la ecuación y2 ? y1 = m(x2 ? x1):

|
Está es la segunda forma de la ecuación de la recta y se utilizacuando se conoce la pendiente y la ordenada al origen, a la cual se lepuede llamar b. También se puede utilizar esta ecuación para conocer la pendiente y la ordenada al origen a partir de una ecuación dada.
Forma segmentaria de la ecuación de la recta (Ecuación simétrica)
Así como a la ordenada al origen se le puede llamar b, a la abscisa al origen se le puede llamar a. Si se plantea como problema encontrar la ecuación de una recta, conocidos a y b (la abscisa y ordenada al origen), se conocen dos puntos de la recta los cuales son:
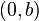 y y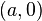 |
Con estos puntos se puede encontrar dicha ecuación, pero primero se debe calcular la pendiente:
 |
Después se sustituye en la ecuación y2 ? y1 = m(x2 ? x1), usando cualquiera de los dos puntos, en este caso (a,0):
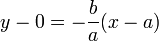 
|
Por último se tiene que dividir toda la ecuación entre el término independiente ab:
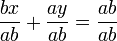 |
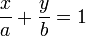 |
Se obtiene la ecuación de la recta en su forma simétrica. Estaecuación se suele utilizar para obtener la ecuación de una recta de laque se conocen sus intersecciones con los ejes y cuando, a partir de laecuación de una recta, se desean conocer los puntos donde dicha rectaintersecta a los ejes.
Forma normal de la ecuación de la recta
Esta es la forma normal de la recta: