Tipos de ángulos y criterios de triángulos: definiciones y propiedades geométricas

Tipos de ángulos y relaciones

Ángulos correspondientes: Son los ángulos que se encuentran en el mismo lado de la secante, formando parejas: A–E, C–G, B–F, D–H.

Alternos internos: Son los ángulos interiores que se encuentran en uno y otro lado de la secante: C–F, D–E.

Alternos externos: Son los ángulos exteriores que se encuentran en uno y otro lado de la secante: A–H, B–G.

Ángulos complementarios: Son dos ángulos cuyas medidas suman grados sexagesimales; es decir, si dos ángulos complementarios son, además, consecutivos, los lados no comunes de estos forman un ángulo recto.

Ángulos suplementarios: Dos ángulos y son suplementarios si suman 180°.

Ángulos adyacentes y opuestos

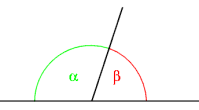
Ángulos adyacentes: Son aquellos ángulos que tienen el vértice y un lado en común, al tiempo que sus otros dos lados son semirrectas opuestas. Se encuentran en la misma recta.

Opuestos por el vértice: Son los ángulos no adyacentes que se forman al cortarse dos rectas y que tienen la misma medida.

Ángulos conjugados: Son dos ángulos cuya suma es igual a 360°.

Clasificación de triángulos y tipos de ángulos en triángulos

Equilátero: Todos los ángulos son iguales.

Isósceles: Dos de sus ángulos son iguales y uno diferente.

Escaleno: Ninguno de sus ángulos es igual a otro.

Acutángulo: Sus tres ángulos son agudos (menos de 90°).

Obtusángulo: Tiene un ángulo mayor de 90°.

Oblicuángulo: Ninguno de sus ángulos interiores es recto.

Agudo: Mide menos de 90°.  Obtuso: Mide más de 90° pero menos de 180°.

Cóncavo: Mide más de 180° y menos de 360° (se aplica a ángulos en general, no a triángulos planos).

Elementos y puntos notables del triángulo

Mediatriz: La mediatriz de un segmento es la recta perpendicular a dicho segmento trazada por su punto medio. Equivalentemente, se puede definir como el lugar geométrico de todos los puntos que son equidistantes a los extremos del segmento. En un triángulo, las mediatrices se cortan en un punto llamado circuncentro, que es el centro de la circunferencia circunscrita a los tres vértices del triángulo.

Ortócentro: Es el punto donde se cortan las tres alturas del triángulo.

Mediana: Son los segmentos que van desde un vértice al punto medio del lado opuesto. El punto donde se cortan las tres medianas de un triángulo se denomina baricentro (o centroide).

Bisectriz: La bisectriz de un ángulo de un triángulo es la semirrecta que divide ese ángulo en dos partes iguales y llega hasta el lado opuesto. El punto donde se cortan las tres bisectrices se llama incentro, y es el centro de la circunferencia inscrita en el triángulo.

Criterios de congruencia

• ALA (Ángulo-Lado-Ángulo): Dos triángulos son congruentes si tienen iguales dos de sus ángulos respectivos y el lado comprendido entre ellos.
• LAL (Lado-Ángulo-Lado): Dos triángulos son congruentes si tienen dos lados iguales y el ángulo comprendido entre ellos igual.
• LLL (Lado-Lado-Lado): Dos triángulos son congruentes si tienen los tres lados iguales.

Criterios de semejanza

Dos triángulos son semejantes si se cumple al menos una de las siguientes condiciones:

• Tienen dos ángulos iguales.
• Tienen un ángulo igual comprendido por lados proporcionales.
• Tienen los tres lados proporcionales (razón constante entre lados correspondientes).

(Contenido corregido y reorganizado para mejorar la claridad y la legibilidad; se han respetado todas las imágenes y etiquetas originales.)