Movimientos en el Plano: Vectores, Traslaciones, Giros y Simetrías

Enviado por Programa Chuletas y clasificado en Plástica y Educación Artística

Escrito el 18 de Julio de 2024 en español con un tamaño de 9,24 KB

Suma de vectores

La suma de dos vectores, 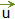y 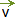, es otro vector, 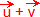, que podemos construir de dos formas:

Situando los vectores 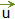y 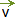con origen en el mismo punto. El vector 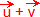queda entonces sobre la diagonal mayor del paralelogramo construido sobre los vectores sumandos.
Haciendo coincidir el origen del vector 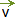con el extremo de 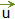. El vector 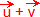tiene como origen el origen de 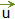y como extremo el de .

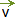Coordenadas de un vector

Un vector 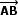está determinado por dos puntos del plano, A(x₁,y₁) que es su ORIGEN y B(x₂,y₂) que es su EXTREMO. Las coordenadas de 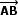son las de B menos las de A: (x₂ - x₁ , y₂ - y₁)

Un vector tiene MÓDULO que es la distancia entre el origen y el extremo, DIRECCIÓN que es la recta que pasa por origen y extremo o cualquier recta paralela a ella y SENTIDO que es el que va desde el origen hacia el extremo y lo marca la flecha.

Traslaciones

Traslación según un vector

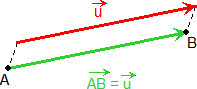
Una traslación de vector 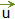es un movimiento que transforma cada punto A del plano, en otro punto B de manera que el vector 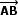es igual al vector .

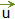Una traslación es un movimiento directo (conserva la orientación) e isomorfo (no cambia la forma de las figuras)

Composición de traslaciones

Dos traslaciones, de vectores 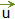y 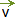, se pueden componer para formar una traslación de vector .

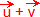Mediante la composición de traslaciones es posible componer interesantes frisos o cenefas. En la escena de la derecha puedes observar algunos.

Giros

Giro de centro O y ángulo α

Un giro, de centro un punto O y amplitud un ángulo α, transforma cada punto P del plano en otro punto P' de modo que el ángulo POP' es igual a α y las distancias OP y OP' son iguales.

Debes tener en cuenta que un giro puede tener orientación positiva (contraria a las agujas del reloj) o negativa.

Simetría respecto a un punto

Una simetría central, o simetría respecto a un punto O, es un giro de centro O y amplitud 180º. Transforma pues, cada punto P en otro punto P' de modo que el ángulo POP' es igual a 180º y las distancias OP y OP' son iguales.

Si al aplicar a una figura una simetría de centro O la figura no varía, O se dice que es su centro de simetría.

Figuras invariantes de orden n

Si al girar una figura con centro en un punto O y según un ángulo menor que 360º, coincide con si misma, el punto O se dice que es centro de giro de la figura.

Si al aplicar a una figura un giro de 360º alrededor de su centro de giro se producen n coincidencias, dicho centro se dice de orden ny la figura invariante de orden n.

4. Simetría axial

Simetría de eje e

Una simetría respecto a un eje e es un movimiento que transforma cada punto P del plano en otro P' de modo que la recta e es mediatriz del segmento de extremos P y P'.

Según esta definición, debe cumplirse que:

La recta e debe ser perpendicular al segmento PP'
La distancia de P a la recta e será igual que la distancia de P' a dicha recta.

Una simetría axial es un movimiento inverso. Observa en la escena cómo se modifica el sentido de giro de la figura.

Figuras con eje de simetría

Hay figuras que son invariantes (no se modifican) al aplicarles una simetría axial. En ese caso, el eje de la misma se llama eje de simetría de la figura. Fíjate en el ejemplo inferior.

Una figura puede tener varios ejes de simetría. Observa el hexágono de la escena de la derecha y algunos de sus ejes de simetría.

Composición de simetrías axiales

La aplicación consecutiva de dos simetrías axiales, de ejes e y e', da lugar a un nuevo movimiento que depende de la situación relativa de los ejes e y e':

Si los ejes e y e' son paralelos, el resultado es una traslación.

Si los ejes e y e' se cortan en un punto, la composición da lugar a un giro alrededor de dicho punto.

Como tanto una traslación como un giro son movimientos directos, el resultado decomponer dos simetrías axiales es unmovimiento directo.

Entradas relacionadas:

Etiquetas: