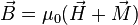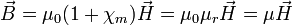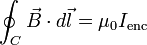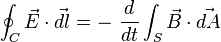Leyes Fundamentales del Electromagnetismo: Ampère y Faraday

Enviado por Programa Chuletas y clasificado en Física

Escrito el 19 de Junio de 2025 en español con un tamaño de 7,9 KB

Leyes Fundamentales del Electromagnetismo

En física del magnetismo, la ley de Ampère, descubierta por André-Marie Ampère en 1826,¹ relaciona un campo magnético estático con la causa que lo produce: una corriente eléctrica estacionaria. James Clerk Maxwell la corrigió posteriormente y ahora es una de las ecuaciones de Maxwell, formando parte del electromagnetismo de la física clásica.

En su forma original, la Ley de Ampère relaciona el campo magnético con la corriente eléctrica que lo genera.

La Ley se puede escribir de dos maneras: la "forma integral" y la "forma diferencial". Ambas formas son equivalentes y se relacionan por el teorema de Stokes.

Forma Integral de la Ley de Ampère

Establece que la integral de línea del campo H sobre cualquier trayectoria cerrada es exactamente igual a la corriente constante encerrada por dicha trayectoria. También, dada una superficie abierta S por la que atraviesa una corriente eléctrica I, y dada la curva C, curva contorno de la superficie S, la forma original de la ley de Ampère para medios materiales es la siguiente:

$\oint_C \vec{H} \cdot d\vec{l} = \int\!\!\!\!\int_S \vec{J} \cdot d \vec{S} = I_{\mathrm{enc}}$

donde:

$\vec{H}$ es la intensidad del campo magnético,

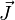$\vec{J}$ es la densidad de corriente eléctrica,

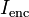$I_{\mathrm{enc}} \,$ es la corriente encerrada en la curva C.

Y se lee: La circulación del campo $\vec{H}$ a lo largo de la curva C es igual al flujo de la densidad de corriente sobre la superficie abierta S, de la cual C es el contorno.

En presencia de un material magnético, aparecen campos de magnetización propios del material, análogamente a los campos de polarización que aparecen en el caso electrostático en presencia de un material dieléctrico bajo un campo eléctrico.

Definición:

$\vec{H}= \frac {\vec{B}} {\mu_0} - \vec{M}$

$\vec{B}=\mu_0(\vec{H} + \vec{M})$

$\vec{B}=\mu_0(1+\chi_m)\vec{H}=\mu_0 \mu_r \vec{H}=\mu \vec{H}$

donde:

$\vec{B}$ es la densidad de flujo magnético,

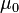$\mu_0\,$ es la permeabilidad magnética del vacío,

$\mu_r\,$ es la permeabilidad magnética del medio material,

Luego, $\mu=\mu_0\mu_r \,$ es la permeabilidad magnética total.

$\vec{M}$ es el vector magnetización del material debido al campo magnético.

$\chi_m\,$ es la susceptibilidad magnética del material.

Un caso particular de interés es cuando el medio es el vacío ( $\mu=\mu_0\,$ , o sea, $\vec{B} = \mu_0 \vec{H} \$ ):

$\oint_C \vec{B} \cdot d\vec{l} = \mu_0 I_{\mathrm{enc}}$

Forma Diferencial de la Ley de Ampère

A partir del teorema de Stokes, esta ley también se puede expresar de forma diferencial:

$\vec\nabla\times\vec H = \vec J$

donde:

$\vec\nabla\times$ es el operador rotacional

$\vec J$ es la densidad de corriente que atraviesa el conductor.

Ley de Inducción Electromagnética de Faraday

La Ley de inducción electromagnética de Faraday (o simplemente Ley de Faraday) se basa en los experimentos que Michael Faraday realizó en 1831 y establece que el voltaje inducido en un circuito cerrado es directamente proporcional a la rapidez con que cambia en el tiempo el flujo magnético que atraviesa una superficie cualquiera con el circuito como borde:¹

$\oint_C \vec{E} \cdot \vec{dl} = - \ { d \over dt } \int_S \vec{B} \cdot \vec{dA}$

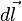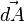donde $\vec{E}$ es el campo eléctrico, $d\vec{l}$ es el elemento infinitesimal del contorno C, $\vec{B}$ es la densidad de campo magnético y S es una superficie arbitraria, cuyo borde es C. Las direcciones del contorno C y de $\vec{dA}$ están dadas por la regla de la mano derecha.

La permutación de la integral de superficie y la derivada temporal se puede hacer siempre y cuando la superficie de integración no cambie con el tiempo.

Por medio del teorema de Stokes puede obtenerse una forma diferencial de esta ley:

$\nabla \times \vec{E} = -\frac{\partial \vec{B}} {\partial t}$

Esta es una de las ecuaciones de Maxwell, las cuales conforman las ecuaciones fundamentales del electromagnetismo. La Ley de Faraday, junto con las otras leyes del electromagnetismo, fue incorporada en las ecuaciones de Maxwell, unificando así el electromagnetismo.

En el caso de un inductor con N vueltas de alambre, la fórmula anterior se transforma en:

V_ε $=-N{d \Phi \over d t}$

donde V_ε es el voltaje inducido y dΦ/dt es la tasa de variación temporal del flujo magnético Φ. La dirección del voltaje inducido (el signo negativo en la fórmula) se debe a la ley de Lenz.

Entradas relacionadas:

Etiquetas: