Geometría de Bisectrices y Construcción de Ángulos: Métodos Esenciales

Construcción de Bisectrices y Ángulos Notables

Bisectriz de un Ángulo Curvilíneo

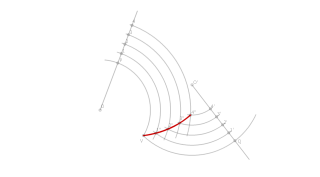
La bisectriz de un ángulo curvilíneo determina el lugar geométrico de los puntos del plano que equidistan de los dos arcos que lo forman. Para trazarla, se siguen los siguientes pasos:

• Se trazan dos arcos de radio arbitrario con centros en O1 y O2.
• Se trazan dos semirrectas con extremos en O1 y O2, y se dividen en el mismo número de partes iguales (por ejemplo, 4).
• Con centro en O1 y O2 respectivamente, se trazan arcos concéntricos que pasen por las divisiones 1, 2, 3 y 4 de las semirrectas.
• Las intersecciones de dos arcos correspondientes a la misma división determinan los puntos de la bisectriz curvilínea.

Bisectriz de un Ángulo Mixtilíneo

Un ángulo mixtilíneo es aquel determinado por una recta y un arco concurrentes. Su bisectriz determina el lugar geométrico de los puntos del plano que equidistan de la recta y el arco.

Sean la recta r y el arco de centro O que corta a la recta r en el punto A. Para trazar su bisectriz:

1. Se traza una perpendicular s a la recta r por un punto cualquiera de esta.
2. Se traslada sobre s una misma medida varias veces (por ejemplo, 4 divisiones).
3. Por los puntos 1, 2, 3 y 4 se trazan paralelas a r.
4. Se traza una semirrecta cualquiera Ot que corta al arco en B.
5. Desde B se trasladan las mismas divisiones que en la recta s.
6. Por los puntos 1, 2, 3 y 4 se trazan los arcos concéntricos, y sus intersecciones con las paralelas determinan los puntos de la bisectriz.

Construcción de Ángulos Notables y sus Bisectrices

La construcción de ángulos específicos a menudo se basa en la bisectriz de otros ángulos conocidos.

Ángulos de 45° y 22°30’

• El ángulo de 45° es la bisectriz del ángulo de 90°.
• El ángulo de 22°30’ es la bisectriz del ángulo de 45°.

Ángulos de 60° y 30°

• Para calcular el ángulo de 60°, con centro en O y A se trazan arcos de igual radio, que se cortan en B.
• El ángulo de 30° se obtiene al calcular la bisectriz del ángulo de 60°.
• El suplementario de 30° es 150°.
• Calculamos la bisectriz del ángulo de 30° para obtener 15°. El suplementario de 15° es 165°.

Ángulos de 75° y 37°30’

• El ángulo de 75° se puede calcular restándole 15° al de 90°, o sumando 15° al de 60°.
• El suplementario de 75° es 105°.
• El ángulo de 37°30’ es la mitad del de 75°.

Ángulo de 120°

• El ángulo de 120° es igual a la suma de dos ángulos de 60°, o el suplementario de 60°.

Trisección del Ángulo Recto

La trisección del ángulo recto es una construcción geométrica clásica:

Sea un ángulo recto de vértice V. Con centro en el vértice V, se traza un arco de radio arbitrario que corta los lados del ángulo en los puntos A y B. Con centro en A y B, se trazan dos arcos de radio igual a VA que cortan el arco anterior en los puntos C y D. Las semirrectas que pasan por el vértice V del ángulo y por los puntos C y D dividen el ángulo recto en tres partes iguales.

Bisectriz de un Ángulo con Vértice Fuera de los Límites del Dibujo

Método 1: Intersección de Bisectrices Auxiliares

Dadas las rectas r y s, trazamos una recta cualquiera t que las corte en A y B, respectivamente. Trazamos las bisectrices de los ángulos determinados por la recta t con las rectas r y s, obteniendo los puntos C y D. Se unen C con D y se obtiene la bisectriz buscada.

Método 2: Uso de Rectas Paralelas

Se trazan rectas paralelas a las dadas, a una distancia igual en ambos casos (aplicando los métodos vistos anteriormente), de modo que se corten dentro de los límites del dibujo. Luego, se calcula la bisectriz de las rectas paralelas.

Recta Convergente

Por un punto P, trazamos dos rectas cualesquiera PM y PN, que cortan a r y s en los puntos M y N, respectivamente. Se traza el triángulo MNP.

Tipos de Triángulos

Este apartado introduce la clasificación de los triángulos según sus lados y ángulos.