Fundamentos de Potenciación y Proporcionalidad Inversa en Matemáticas

Fundamentos y Propiedades de la Potenciación

La potenciación es una operación matemática que consiste en multiplicar un número (la base) por sí mismo varias veces (indicadas por el exponente). A continuación, se detallan las reglas esenciales de los exponentes.

Reglas Básicas de Exponentes

• Exponente Uno

  Todo número elevado a la potencia de uno es igual a sí mismo. Ejemplo: $5^1 = 5$.

• Exponente Cero

  Todo número (distinto de cero) elevado a la potencia de cero es igual a uno. Ejemplo: $X^0 = 1$.

Operaciones con Potencias de Igual Base

Multiplicación de Potencias con la Misma Base

El producto de potencias con la misma base es igual a otra potencia con la misma base, elevada a la suma de los exponentes.

$$2^4 \cdot 2^2 \cdot 2^4 = 2^{(4+2+4)} = 2^{10}$$

División de Potencias con la Misma Base

El cociente de potencias con la misma base es igual a otra potencia con la misma base, elevada a la resta de los exponentes.

$$4^4 / 4^2 = 4^{(4-2)} = 4^2$$

Operaciones con Potencias de Igual Exponente

Multiplicación de Potencias con el Mismo Exponente

El producto de dos o más potencias con bases diferentes e igual exponente es igual al producto de las bases, elevado al mismo exponente.

$$(3 \cdot 2 \cdot 3)^2 = 18^2$$

División de Potencias con el Mismo Exponente

El cociente entre dos potencias con bases diferentes es igual a la división de las bases, elevado al mismo exponente.

$$8^2 : 2^2 = (8 : 2)^2 = 4^2$$

Potencia de una Potencia

La potencia de una potencia resulta en otra potencia con la misma base, elevada al producto de los exponentes.

$$(8^3)^3 = 8^{(3 \cdot 3)} = 8^9$$

Exponentes Especiales y Radicales

Raíz de una Potencia (Exponente Fraccionario)

Cuando se tiene dentro de una raíz un número elevado a un exponente, este se puede expresar como una potencia de exponente fraccionario, donde el exponente es el numerador y el índice de la raíz es el denominador.

Ejemplo de cálculo relacionado: $2^{1/4} - 2.25$. El cuatro se multiplica por dos y el resultado se suma con el número de arriba, creando así $1/4$. Para simplificar, tendríamos que hacer cuatro al cuadrado de nueve, de ahí se saca el dos punto veinticinco.

Potencia Negativa

Si se tiene una base con exponente negativo, se debe tomar la unidad dividida entre la base, que será elevada con el signo del exponente en positivo (el inverso de la base).

$$10^{-3} = \frac{1}{10^3}$$ y $$10^{-7} = \frac{1}{10^7}$$ .

Potencia Positiva (Exponente Natural)

La potencia de exponente natural de un número entero positivo es igual a multiplicar dicho número por sí mismo tantas veces como indique el exponente. Si la base es positiva, el resultado es positivo.

Proporcionalidad Inversa y Regla de Tres

Definición de Proporcionalidad Inversa

Dos magnitudes son inversamente proporcionales si, al multiplicar (o dividir) una de ellas por un número distinto de cero, la otra resulta dividida (o multiplicada) por ese mismo número.

Es decir, es proporcionalidad inversa si, por ejemplo, al doble de la cantidad de una magnitud le corresponde la mitad de la cantidad de la otra.

Aplicación: La Regla de Tres Inversa

Esta técnica se aplica a los problemas de proporcionalidad en los cuales se conocen tres de los cuatro datos que componen las proporciones y se requiere calcular el cuarto (la incógnita).

El procedimiento general para la Regla de Tres Inversa es:

1. Primero, se establece la relación conocida entre la Magnitud A y la Magnitud B.
2. Después, se escribe la relación que se desea calcular.

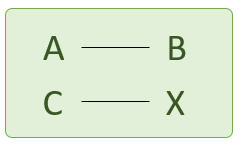
Donde C es un valor de la magnitud A, y X es el valor de la magnitud B que tenemos que hallar.