Funciones Continuas y Discontinuas: Definiciones y Ejemplos

Continuidad

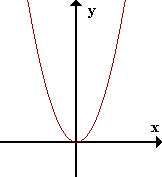\(f(x) = x^2\)

Intuitivamente, la continuidad significa que un pequeño cambio en la variable \(x\) implica sólo un pequeño cambio en el valor de \(f(x)\), es decir, la gráfica consiste de un sólo trozo de curva.

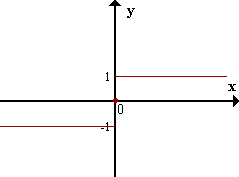\(f(x) = \text{sgn} \, x\)

En contraste, una gráfica como la de la función \(f(x) = \text{sgn} \, x\) (signo de \(x\)) que consiste de pedazos de curva separados por un vacío en una abscisa exhibe allí una discontinuidad.

La continuidad de la función \(f(x)\) para un valor \(a\) significa que \(f(x)\) difiere arbitrariamente poco del valor \(f(a)\) cuando \(x\) está suficientemente cerca de \(a\).

Expresemos esto en términos del concepto de límite...

Definición

Continuidad

Una función \(f(x)\) es continua en un punto \(a\) si \(\lim_{x \to a} f(x) = f(a)\).

Nota: Observar que debe existir \(f(a)\) y debe existir el \(\lim_{x \to a} f(x)\) y debe ser igual a \(f(a)\).

Ejemplos de Discontinuidad

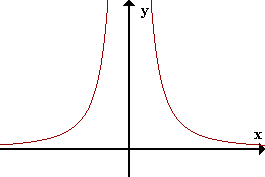\(f(x) = 1/x^2\) Discontinua en \(x=0\) (No existe \(f(0)\))

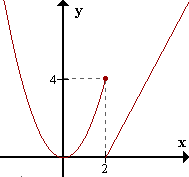\(f(x) = \begin{cases} x^2 & \text{si } x \leq 2 \\ 2x - 4 & \text{si } x > 2 \end{cases}\) Discontinua en \(x=2\). Si bien existe \(f(2)\), no existe \(\lim_{x \to 2} f(x)\), pues \(\lim_{x \to 2^-} f(x) = 4\) y \(\lim_{x \to 2^+} f(x) = 0\)

Sin embargo, si miramos la función para \(x\) próximos a 2 pero menores, e ignoramos los \(x\) mayores que 2, la función es continua en 2 "por la izquierda".

Definición

Continuidad por la Izquierda

Una función \(f(x)\) es continua por la izquierda en el punto \(a\) si existe \(f(a)\) y \(\lim_{x \to a^-} f(x) = f(a)\).

Definición

Continuidad por la Derecha

Una función \(f(x)\) es continua por la derecha en el punto \(a\) si existe \(f(a)\) y \(\lim_{x \to a^+} f(x) = f(a)\).

La función anterior es continua por la izquierda en \(x=2\), pero no por la derecha.

Definición

Continuidad en un Intervalo Cerrado \([a,b]\)

Una función \(f(x)\) es continua en un intervalo cerrado \([a,b]\) si:

• \(f\) es continua en \(a\) por la derecha
• \(f\) es continua en \(b\) por la izquierda
• \(f\) es continua en \(x\), para todo \(x\) perteneciente al intervalo abierto \((a,b)\)

Clasificación de Discontinuidades

Evitable

Caso A:

No existe \(f(a)\) pero existe \(\lim_{x \to a} f(x)\).

Ejemplo:

\(f(x) = e^{-1/x^2} + 2\)

No existe \(f(0)\) pues anula un denominador.

\(\lim_{x \to 0^-} f(x) = \lim_{x \to 0^+} f(x) = 2\) o sea \(\lim_{x \to 0} f(x) = 2\)

Podemos extender la definición de la función, asignándole en el punto \(a\) el valor del límite, con lo cual la función se torna continua. Por ello este tipo de discontinuidad se denomina evitable.

Caso B:

Existe \(f(a)\) y existe \(\lim_{x \to a} f(x) = b\) pero \(b \neq f(a)\).
(Existe \(f(a)\) pero es distinto al valor del límite).

Ejemplo:

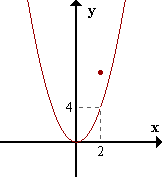\(f(x) = \begin{cases} x^2 & \text{si } x \neq 2 \\ 8 & \text{si } x = 2 \end{cases}\)

\(f(2) = 8\)
\(\lim_{x \to 2} f(x) = 4\)

Asignándole a la función el valor 4 en \(x=2\), se elimina la discontinuidad.

No Evitable

1ª especie:

\(\lim_{x \to a^-} f(x) \neq \lim_{x \to a^+} f(x)\).
(Los límites laterales son distintos).

Ejemplo:

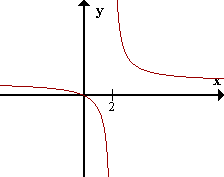\(f(x) = x/(x - 2)\)

\(\lim_{x \to 2^-} f(x) = -\infty\)
\(\lim_{x \to 2^+} f(x) = +\infty\)

2ª especie:

No existe \(\lim_{x \to a^-} f(x)\) o no existe \(\lim_{x \to a^+} f(x)\).
(No existe por lo menos uno de los límites laterales).

Ejemplo:

______ f(x) = \|x^2 - 4

En \(x=-2\) y \(x=2\) la función presenta discontinuidades no evitables de 2ª especie. No existe \(\lim_{x \to -2^+} f(x)\) y no existe \(\lim_{x \to 2^-} f(x)\).

Operaciones con Funciones Continuas

Si \(f\) y \(g\) son funciones continuas en \(x=a\), la suma, multiplicación y cociente de \(f\) y \(g\) (con \(g(a) \neq 0\)) son funciones continuas en \(x=a\).

\(H) \ f(x)\) es continua en \(x=a\).
\(g(x)\) es continua en \(x=a\).
\(T) \ f(x) + g(x)\) es continua en \(x=a\).

Demostración

Por definición de continuidad,

existe \(f(a)\) y existe \(\lim_{x \to a} f(x) = f(a)\)
existe \(g(a)\) y existe \(\lim_{x \to a} g(x) = g(a)\)

\(=>\) por teorema del límite de la suma de funciones, el límite de una suma de funciones es igual a la suma de los límites de cada función, si éstos son finitos.

\(\lim_{x \to a} f(x) + g(x) = f(a) + g(a)\)

\(=>\) por definición de continuidad \(f(x) + g(x)\) es continua en \(x=a\).

Análogamente se prueba la continuidad del producto y el cociente.

Teorema

Continuidad de la Función Compuesta

\(H) \ f\) es continua en \(x=a\).
\(g\) es continua en \(x=f(a)\).
\(T) \ g \circ f\) es continua en \(x=a\).

Demostración:

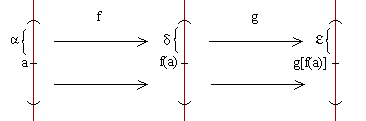
Queremos demostrar que \(\lim_{x \to a} g[f(x)] = g[f(a)]\), o sea, por definición de límite, queremos probar que, dado \(\varepsilon > 0\) existe \(\delta > 0\) tal que para todo \(x\) perteneciente al \(E^*_{a,\delta}\) \(g[f(x)]\) pertenece al \(E_{g[f(a)],\varepsilon}\).

Por hipótesis \(g\) es continua en \(f(a)\) \(=>\) por definición de continuidad \(\lim_{x \to f(a)} g(x) = g[f(a)]\) \(=>\) por definición de límite, dado \(\varepsilon > 0\) existe \(\delta > 0\) tal que...

para todo \(x\) perteneciente al \(E^*_{f(a),\delta}\) \(g(x)\) pertenece al \(E_{g[f(a)],\varepsilon}\) (1)

Por hipótesis \(f\) es continua en \(a\) \(=>\) por definición de continuidad \(\lim_{x \to a} f(x) = f(a)\), es decir que (por definición de límite) si tomamos el número \(\delta\) de (1), existe \(\alpha > 0\) tal que...

para todo \(x\) perteneciente al \(E^*_{a,\alpha}\) \(f(x)\) pertenece al \(E_{f(a),\delta}\) (2)

De (1) y (2) se deduce que:
Dado \(\varepsilon > 0\) existe \(\alpha > 0\) / para todo \(x\) perteneciente al \(E^*_{a,\alpha}\) \(g[f(x)]\) pertenece al \(E_{g[f(a)],\varepsilon}\).