Fórmulas Matemáticas

Fórmulas Matemáticas Elementales

• Ecuación de primer grado
• Ecuación de segundo grado
• Sistema de ecuaciones
• Sucesiones aritméticas
• Ecuación recta
• Distancia entre dos puntos
• Ecuación circunferencia
• Coordenadas polares

En esta página se incluyen algunas fórmulas matemáticas elementales. La demostración de algunas de estas fórmulas se encuentra en la lección Demostración de fórmulas matemáticas.

Resolución de la Ecuación de Primer Grado

Una ecuación de primer grado es una ecuación del tipo:

ax+b=0ax+b=0

donde aa y bb son números cualesquiera.

Si xx es un número real, la ecuación puede tener 0, 1 o infinitas soluciones, dependiendo de los valores de aa y bb:

• Si a=0a=0 y b=0b=0, la ecuación tiene infinitas soluciones.
• Si a=0a=0 y b≠0b≠0, la ecuación no tiene solución.
• Si a≠0a≠0, la ecuación tiene una solución única: x1=−bax1=-ba.

Resolución de la Ecuación de Segundo Grado

Una ecuación de segundo grado es una ecuación del tipo:

ax2+bx+c=0ax2+bx+c=0

donde aa, bb y cc son números cualesquiera.

Nota: Para que se trate de una ecuación de segundo grado, aa tiene que ser distinta de 0. Si a=0a=0, se trataría de una ecuación de primer grado.

Si xx es un número real, la ecuación puede tener 0, 1 o 2 soluciones, dependiendo del valor de b2−4acb2-4ac:

• Si b2−4ac0b2-4ac, la ecuación no tiene solución
• Si b2−4ac=0b2-4ac=0, la ecuación tiene una solución doble: x1=−b2ax1=-b2a
• Si b2−4ac>0b2-4ac>0, la ecuación tiene dos soluciones distintas: x1=−b+√b2−4ac2ax1=-b+b2-4ac2a, x2=−b−√b2−4ac2ax2=-b-b2-4ac2a

Resolución del sistema de ecuaciones de primer grado

Un sistema de ecuaciones de primer grado es un sistema del tipo:

{a1x+b1y=c1a2x+b2y=c2{a1x+b1y=c1a2x+b2y=c2

donde a1a1, b1b1, c1c1, a2a2, b2b2 y c2c2 son números cualesquiera.

Las soluciones de un sistema de ecuaciones se suelen expresar escribiendo:

x=x1x=x1 e y=y1y=y1

o escribiendo:

(x1,y1)(x1,y1)

Un sistema de ecuaciones de primer grado puede tener 0, 1 o infinitas soluciones, dependiendo del valor de a1b2−a2b1a1b2-a2b1 y de c1c1 y c2c2:

• Si a1b2−a2b1=0a1b2-a2b1=0 y c1≠c2c1≠c2, el sistema no tiene solución.
• Si a1b2−a2b1=0a1b2-a2b1=0 y c1=c2c1=c2, el sistema tiene infinitas soluciones del tipo (x,c1−a1xb1)(x,c1-a1xb1) donde xx es cualquier número real.
• Si a1b2−a2b1≠0a1b2-a2b1≠0, la ecuación tiene una única solución: (c1b2−c2b1a1b2−a2b1,a1c2−a2c1a1b2−a2b1)(c1b2-c2b1a1b2-a2b1,a1c2-a2c1a1b2-a2b1)

Sucesiones aritméticas

Una sucesión artimética (o progresión aritmética) es una serie ordenada de números ...

Un={U0,U1,U2,U3,U4,...}Un={U0,U1,U2,U3,U4,...}

en la que la diferencia entre dos valores (también llamados términos) consecutivos es siempre la misma:

Un+1−Un=dUn+1-Un=d

Por ejemplo, la sucesión ...

Un={10,13,16,19,22,...}Un={10,13,16,19,22,...}

es una sucesión aritmética de diferencia 3 porque la diferencia entre dos términos consecutivos es siempre 3:

U1−U0=13−10=3U1-U0=13-10=3

U2−U1=16−13=3U2-U1=16-13=3

U3−U2=19−16=3U3-U2=19-16=3

Es importante señalar que el índice n que identifica a los términos de la sucesión empieza desde 0, es decir, que el primer término de la sucesión es el término U0U0, el segundo término es el término U1U1, etc.

Término general de una sucesión aritmética

Se puede calcular cualquier término de una sucesión aritmética calculando todos los valores intermedios o mediante la fórmula del término general de una sucesión aritmética:

Un=U0+n⋅dUn=U0+n⋅d

La expresión del término general de una sucesión aritmética permite calcular fácilmente tantos valores como deseemos.

Por ejemplo, si queremos generar los veinte primeros valores de la sucesión {7, 12, 17, 22, 27, 32, ...} habrá que tener en cuenta que se trata de una sucesión aritmética cuyo primer término es 7 y cuya diferencia es 5, por lo tanto el término general es: Un=7+5⋅nUn=7+5⋅n. Para generar en Python los primeros 20 valores bastaría escribir el programa:

for i in range(20):
    print(7 + 5*n)

O por ejemplo, si queremos generar los treinta primeros valores de la sucesión {100, 98, 96, 94, ...} habrá que tener en cuenta que se trata de una sucesión aritmética cuyo primer término es 100 y cuya diferencia es -2, por lo tanto el término general es: Un=100−2⋅nUn=100-2⋅n. Para generar en Python los primeros 30 valores bastaría escribir el programa:

for i in range(30):
    print(100 - 2*n)

Ecuación de la recta que pasa por dos puntos

La ecuación de la recta que pasa por dos puntos A(x1,y1)A(x1,y1) y B(x2,y2)B(x2,y2) es:

• Si la recta es una recta vertical, es decir, si las abcisas coinciden (x1=x2x1=x2), la ecuación es x=x1x=x1
• Si la recta es una recta horizontal, es decir, si las ordenadas coinciden (y1=y2y1=y2), la ecuación es y=y1y=y1
• Si la recta es una recta oblicua, la ecuación es:
  y−y1x−x1=y2−y1x2−x1y-y1x-x1=y2-y1x2-x1
  que también se puede escribir, expresando yy en función de xx, como:
  y=y2−y1x2−x1x+x2y1−x1y2x2−x1y=y2-y1x2-x1x+x2y1-x1y2x2-x1

Distancia entre dos puntos

La distancia dd entre los puntos A(x1,y1)A(x1,y1) y B(x2,y2)B(x2,y2) es:

d=√(x2−x1)2+(y2−y1)2d=(x2-x1)2+(y2-y1)2

Ecuación de la circunferencia

La ecuación de la circunferencia de centro C(x1,y1)C(x1,y1) y radio RR es:

(x−x1)2+(y−y1)2=R2(x-x1)2+(y-y1)2=R2

que también se puede escribir expresando yy en función de xx como:

y=y1±√R2−(x−x1)2y=y1±R2-(x-x1)2

... teniendo en cuenta que xx toma valores entre x1−Rx1-R y x1+Rx1+R, es decir:

x1−R≤x≤x1+Rx1-R≤x≤x1+R

Nota: El ± de la fórmula anterior significa que para cada valor de x hay dos posibles valores de y, que se calculan sumando o restando la raíz cuadrada.

Coordenadas polares

Las coordenadas polares consisten en identificar un punto por su distancia al origen (R) y el ángulo (α) que forma el semieje X con la línea que une el origen con el punto:

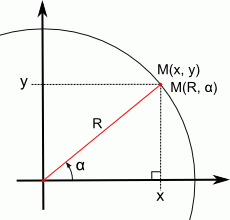
Las relaciones entre coordenadas polares y coordenadas cartesianas son:

{x=R⋅cos(α)y=R⋅sin(α){x=R⋅cos(α)y=R⋅sin(α) y {R=√x2+y2α=arctan(yx){R=x2+y2α=arctan(yx)

y también se dan las relaciones α=arccos(xR)α=arccos(xR)y α=arcsin(yR)α=arcsin(yR)

Si la circunferencia no está centrada en el origen:

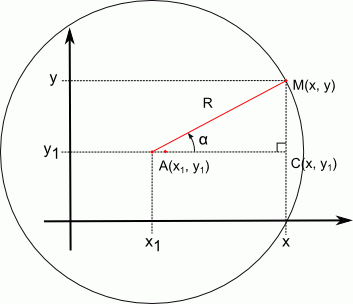
las relaciones entre coordenadas polares y cartesianas son:

{x=x1+R⋅cos(α)y=y1+R⋅sin(α){x=x1+R⋅cos(α)y=y1+R⋅sin(α) y ⎧⎪ ⎪⎨⎪ ⎪⎩R=√(x−x1)2+(y−y1)2α=arctan(y−y1x−x1){R=(x-x1)2+(y-y1)2α=arctan(y-y1x-x1)

Última modificación de esta página: 13 de mayo de 2016

Esta página forma parte del curso Temas de Informática por Bartolomé Sintes Marco
que se distribuye bajo una Licencia Creative Commons Reconocimiento-CompartirIgual 4.0 Internacional (CC BY-SA 4.0).