Desarrollo de Programas para el Cálculo de Volúmenes en Programación

Enviado por Programa Chuletas y clasificado en Otras materias

Escrito el 7 de Diciembre de 2024 en español con un tamaño de 7,13 KB

Resumen: Entrega n°7 del curso Bases de la Programación Nivel I.

Codificación aprenderaprogramar.com: CU00108A

Continuamos con otro posible planteamiento de objetivos de programación:

b) Desarrollar un programa para el cálculo de depósitos (volúmenes) de los siguientes tipos:

Esfera seccionada en su base inferior para conseguir una base plana de apoyo.
Cono circular.
Tronco de una pirámide.

Comentarios: problema que mentalmente somos capaces de abarcar con un esquema como el mostrado en la Figura 1.

A la hora de plantear el objetivo, no es imprescindible elaborar un esquema como el anterior.

Es suficiente saber hacer una valoración global respecto a si creemos conocer los condicionantes, métodos y datos de partida, así como si tenemos claros los resultados a mostrar.

Por último, en cuanto al objetivo, desde este momento conviene empezar a pensar en resolver problemas genéricos con variables no fijadas.

Ejemplo: Si habitualmente trabajamos con depósitos de combustible tipo esfera seccionada con una altura eliminada de 2 metros, podríamos "fijar" este parámetro de modo que dejará de ser un dato de entrada. Esto a su vez "simplificaría" el proceso de cálculo al tener una variable menos.

Sin embargo, recomendamos no hacer esto porque a la larga nos supondrá adquirir un mal hábito de programación. Lo adecuado será, pues, programar el caso genérico de un depósito con radio r y altura eliminada h. Si se quiere evitar que el usuario tenga que introducir un valor que se repite (h), podemos hacer que aparezca como predeterminado en la lista de datos de entrada, o bien que se acceda a cambiarlo a través de una opción específica.

A la hora de programar, nos interesa obtener la máxima potencialidad posible para el tiempo y esfuerzo que apliquemos a la tarea. Obtener potencialidad implica que el programa sea capaz de resolver el mayor número de casos y variantes posibles. Por tanto, el programa hay que "abrirlo".

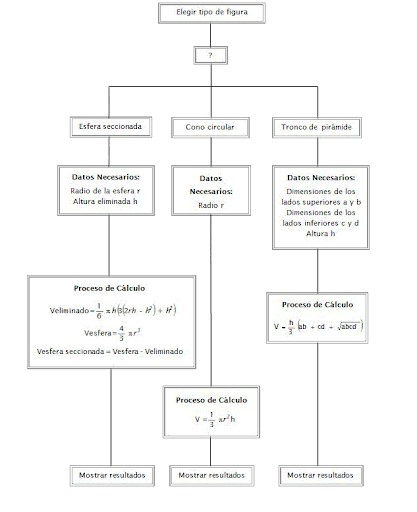
Esquema para un problema de cálculo de volúmenes

Figura 1. Esquema para un problema de cálculo de volúmenes.

El planteamiento de objetivos se resume en el siguiente cuadro:

Proceso	Movimiento tipo	Finalidad
Centrar	Cerrar el problema	Hacer abarcable el objetivo subdividiendo en extensión y complejidad
Enfocar	Abrir el problema	Obtener máxima potencialidad

EJERCICIO

Distintas personas han planteado estos seis objetivos para desarrollar un programa útil para su trabajo. Hacer una valoración de los mismos.

Programa para cálculo de muros de contención de tierras, para ventas de hasta 50 unidades y a 0,55 € / ud para ventas de más de 50 unidades.
Programa para determinar la facturación de un producto que se vende a 0,60 € / ud.
Programa para determinar el peso de una plancha de hierro rectangular a la que se hace una perforación circular.
Programa para simular el disparo de un proyectil que se supone sigue un tiro parabólico.
Programa para el cálculo de edificios de hasta 8 plantas.
Programa para el cálculo de armaduras de muros de hormigón armado con puntera y talón.

SOLUCIÓN

Planteamiento no suficientemente centrado. Existen diferentes tipologías de muros de contención, que a su vez pueden estar afectados por múltiples tipos de carga, etc. Por tanto, problema demasiado extenso.
Problema bien centrado. Como única indicación, recomendamos programarlo partiendo de valores variables en vez de fijos. Es decir, desarrollaremos un programa para determinar la facturación de un producto que se vende a x € / ud para ventas de hasta n unidades y a z € / ud para ventas de más de n uds.
Problema bien centrado y bien enfocado.
Problema bien centrado y bien enfocado. Obviamente es más complejo que el caso de resolver el peso de la plancha de hierro en el que rápidamente se nos ocurren las variables y procedimientos de cálculo.
Problema no centrado. Si se refiere a un cálculo de cimentación, estructura, instalaciones, etc., la cantidad de variantes y su complejidad invitan a subdividir, y mucho.
Planteamiento que puede ser correcto aunque al menos mentalmente deberíamos acotar a un problema concreto (p. ej. muro que soporta un relleno sin talud y sin sobrecargas). Una vez resuelto este programa, podríamos aumentar las posibilidades de cálculo del mismo (p. ej. cargas lineales, cargas en faja, etc).

CU00108A Problemas a resolver en programación de ordenadores.pdf

Proceso

Movimiento tipo
Finalidad
Centrar
Cerrar el problema
Hacer abarcable el objetivo subdividiendo en extensión y complejidad
Enfocar
Abrir el problema
Obtener máxima potencialidad

Proceso

Movimiento tipo
Finalidad
Centrar
Cerrar el problema
Hacer abarcable el objetivo subdividiendo en extensión y complejidad
Enfocar
Abrir el problema
Obtener máxima potencialidad

Entradas relacionadas:

Etiquetas: