Conceptos básicos de Química

Enviado por Chuletator online y clasificado en Química

Escrito el en español con un tamaño de 335,33 KB

Números Cuánticos

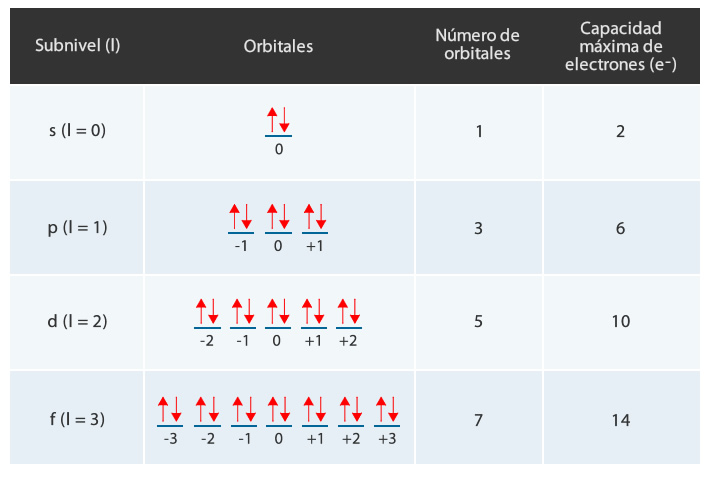
Los cuatro números cuánticos y su significado

Los números cuánticos son valores numéricos que nos indican las características de los electrones de los átomos, esto está basado en la teoría atómica de Neils Bohr que es el modelo atómico más aceptado y utilizado en los últimos tiempos.


Hibridación de Orbitales

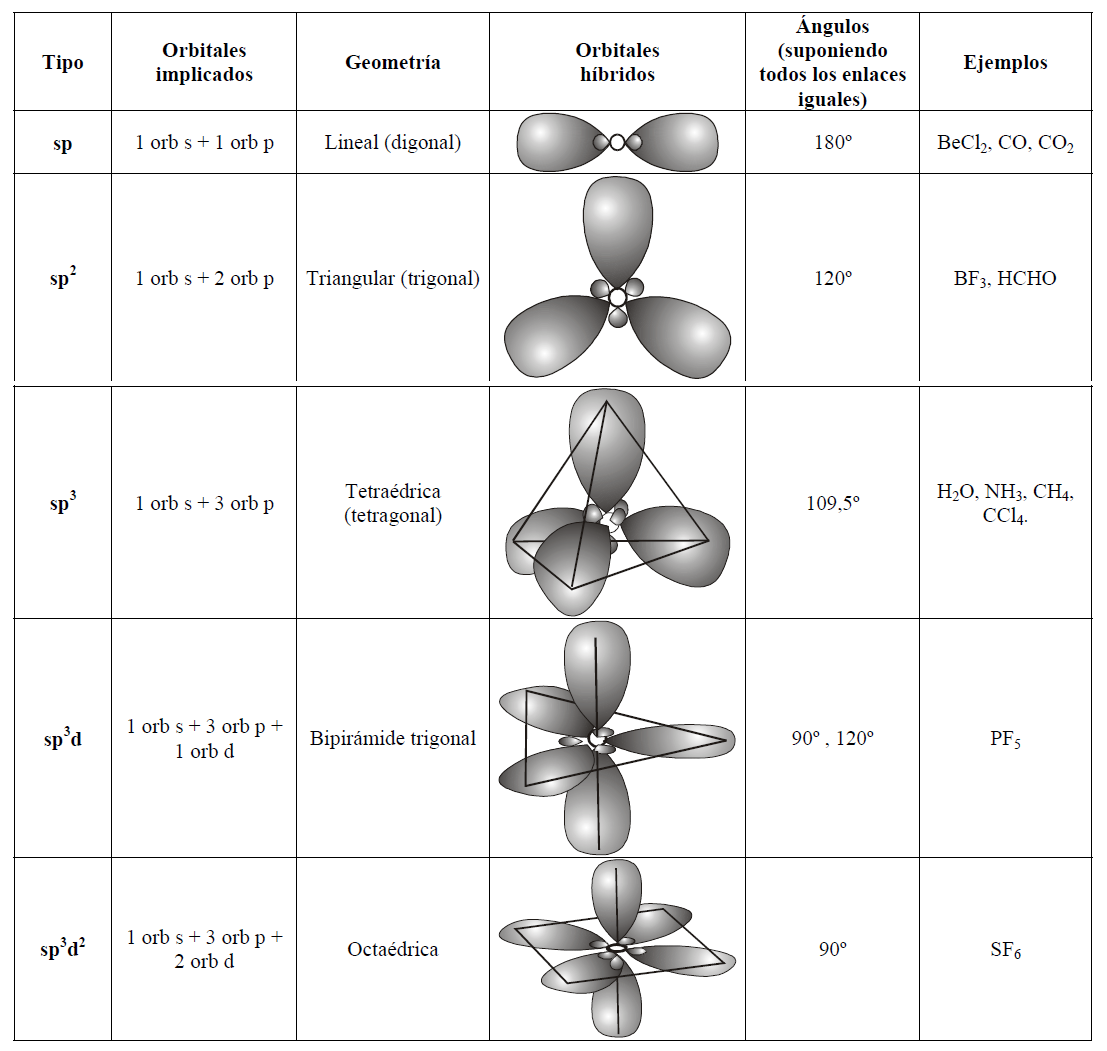
EL FÍSICO LOCO: Teoría de Hibridación

En química, se conoce como hibridación a la interacción de orbitales atómicos dentro de un átomo para formar nuevos orbitales híbridos. Los orbitales atómicos híbridos son los que se superponen en la formación de los enlaces, dentro de la teoría del enlace de valencia, y justifican la geometría molecular. Wikipedia


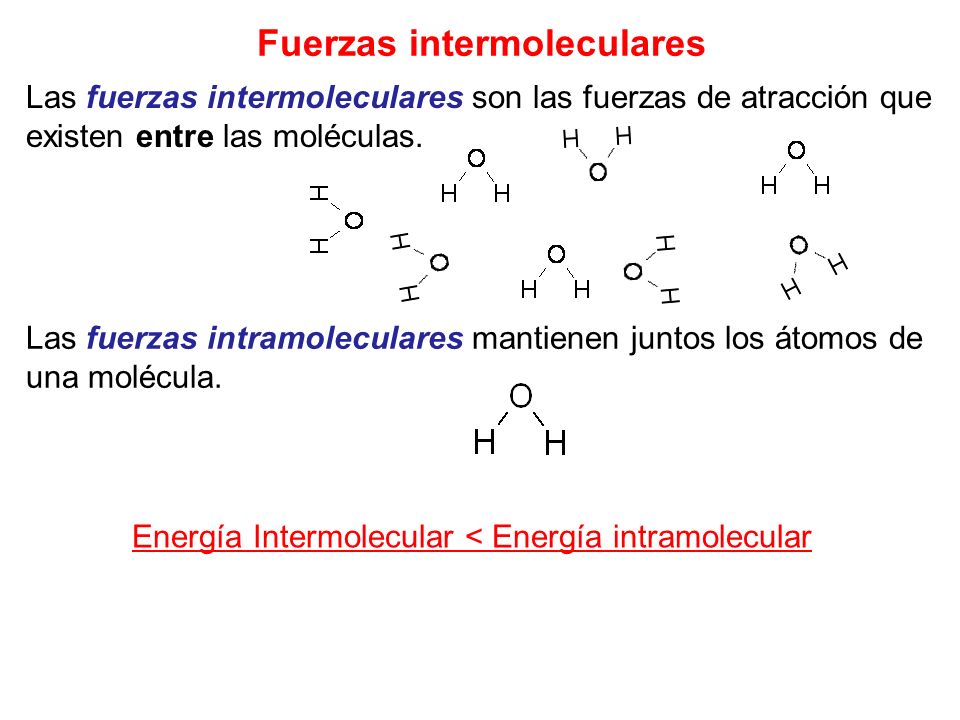
Fuerza Intra e Intermoleculares

Las fuerzas intramoleculares son las que, dentro de la molécula, la mantienen unida, por ejemplo, los enlaces entre los átomos. Las fuerzas intermoleculares son las atracciones entre las moléculas, que determinan muchas de las propiedades físicas de una sustancia.

INTERACCIONES INTRAMOLECULARES E INTERMOLECULARES. - ppt descargar


Reacciones Químicas

Las reacciones químicas suceden cuando se rompen o se forman enlaces químicos entre los átomos. Las sustancias que participan en una reacción química se conocen como los reactivos, y las sustancias que se producen al final de la reacción se conocen como los productos.

💥Tipos de Reacciones Químicas⚠️ [Fácil y Rápido] | Química | - YouTube

Unidad didáctica 3: La química del cuerpo humano - Licenciatura en Enfermería y Obstetricia


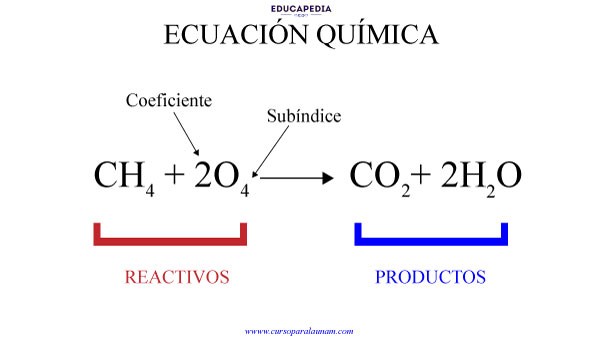
Ecuaciones Químicas

Una ecuación química es una descripción simbólica de una reacción química. Muestra las sustancias que reaccionan (llamadas reactivos) y las sustancias que se originan (llamadas productos). La ecuación química ayuda a visualizar más fácilmente los reactivos y los productos.
LA ENERGÍA Y LAS REACCIONES QUÍMICAS - Curso para la UNAM


Ley de Conservación de la Materia (Valanceo de Ecuaciones)

Esta es la ley de la conservación de la masa, enunciándola de la siguiente manera: «En toda reacción química la masa se conserva, es decir, la masa total de los reactivos es igual a la masa total de los productos». Cuando una vela arde no se gana ni se pierde masa.

Dicho de otra forma, si llenamos un recipiente con agua y lo congelamos, la cantidad de agua no aumenta ni disminuye, únicamente cambia su estado de líquido a sólido. El proceso no altera la masa de los elementos que participan en la reacción, solo provoca una nueva organización en su estructura.
Resultado de imagen para ley de conservación de la materia


Nomenclaturas Inorgánicas

También llamada nomenclatura por atomicidad, estequiométrica o de la IUPAC, consiste en nombrar a las sustancias usando prefijos numéricos griegos que indican la atomicidad de cada uno de los elementos presentes en cada molécula.

IGIj1WWsRxQAAAAASUVORK5CYII=

Karma: 6%
Visitas: 0

Entradas relacionadas:

Etiquetas:
reacciones químicas ley de conservación de la materia ecuaciones químicas nomenclaturas inorgánicas hibridación de orbitales fuerzas intramoleculares números cuánticos