Compendio de Fórmulas Físicas Esenciales: Gravitación, Electromagnetismo y Ondas
Enviado por Chuletator online y clasificado en Física
Escrito el en  español con un tamaño de 21,68 KB
español con un tamaño de 21,68 KB
Campo Gravitatorio
- 1. Ley de Gravitación Universal y Velocidad Orbital
De la igualdad entre la fuerza gravitatoria y la fuerza centrípeta (F_g = F_c):
Si se requiere la velocidad orbital (G \frac{M_{planeta} m_{satélite}}{R^2} = \frac{m_{satélite} v_{orb}^2}{R}v_{orb}):
(Unidades: m/s)v_{orb} = \sqrt{\frac{G M_{planeta}}{R}} = \sqrt{\frac{g_0 R_{planeta}^2}{R}} - 2. Relación entre Constante Gravitacional y Gravedad Superficial
(Se utiliza para sustituir en otras expresiones)G M_{planeta} = g_0 R_{planeta}^2 - 3. Periodo Orbital y Velocidad Orbital
(Útil si se busca el radiov_{orb} = \sqrt{\frac{G M_{planeta}}{R}} = \frac{2\pi R}{T}Ro el periodoT. Unidades: m/s) - 4. Energía Mecánica (
E_m)
(Para calcular la Energía Mecánica. Unidades: J)E_m = E_c + E_p
(SiE_m = \frac{1}{2} m_{satélite} v_{orb}^2 - G \frac{M_{planeta} m_{satélite}}{R} = -\frac{1}{2} \frac{G M_p m_s}{R}v_{orb}no es conocida, se puede sustituir su expresión) - 5. Diferencia de Energía Mecánica (
\Delta E_m)
(Diferencia de Energía Mecánica. Unidades: J)\Delta E_m = E_{mf} - E_{mi} = \frac{1}{2} G M_p m_s \left(\frac{1}{R_i} - \frac{1}{R_f}\right) - 6. Tercera Ley de Kepler
(Ley de Kepler. Útil para calcular el periodo de un planeta\frac{T_p^2}{R_p^3} = \frac{T_t^2}{R_t^3}T_psiT_t = 1año para la Tierra) - 7. Relaciones de Velocidad y Energía en Órbitas Elípticas (Afelio y Perihelio)
\frac{v_p}{v_a} = \frac{R_a}{R_p}\left(\frac{v_a}{v_p}\right)^2 = \left(\frac{R_a}{R_p}\right)^2 = \frac{E_{c, afelio}}{E_{c, perihelio}} - 8. Relación de Energía Potencial en Órbitas Elípticas
\frac{E_{p, afelio}}{E_{p, perihelio}} = \frac{R_p}{R_a}
Campo Eléctrico
- 1. Potencial Eléctrico (
V)
(Potencial eléctrico en un punto A debido a cargas puntuales. Unidades: V)V_a = k \frac{q_1}{r_{a1}} + k \frac{q_2}{r_{a2}} - 2. Campo Eléctrico Resultante (
\vec{E}_{total})
(Campo eléctrico resultante. Unidades: N/C o V/m. Componentes vectoriales:\vec{E}_{total} = \vec{E}_1 - \vec{E}_2 = k \frac{q_1}{r_{a1}^3} \vec{r}_{a1}(i, j, k))
Nota: La expresión vectorialk (q₁ / r³)es para el campo de una carga puntual, y la resta indica superposición. - 3. Trabajo Eléctrico (
W)
(Trabajo realizado por el campo eléctrico para trasladar una cargaW = -q (V_b - V_a)qde A a B. Unidades: J) - 4. Aceleración de una Partícula Cargada
(Aceleración de una partícula cargada en un campo eléctrico. Unidades: m/s²)m_{ión} \vec{a} = q \vec{E}_{total} - 5. Cuantificación de la Carga Eléctrica
(Carga total. Unidades: C.q = n_{electrones} \times 1.6 \times 10^{-19} \text{ C}n_{electrones}es el número de electrones)
Movimiento Armónico Simple y Ondas
- 1. Periodo (
T)
(Periodo. Unidades: s)T = 1 / f - 2. Velocidad Angular (
\omega)
(Velocidad angular. Unidades: rad/s)\omega = 2\pi / T - 3. Velocidad de Propagación de la Onda (
v)
(Velocidad de propagación de la onda. Unidades: m/s)v = \lambda f - 4. Número de Onda (
k)
(Número de onda. Unidades: rad/m. Nota: La constante de elasticidad de un muelle también se denota conk = 2\pi / \lambdak, pero no es estak) - 5. Nivel de Intensidad Sonora (
\beta)
(Nivel de intensidad sonora en decibelios. Unidades: dB)\beta = 10 \log_{10} (I / I_0)
(Ley del inverso del cuadrado para la intensidad)I_2 / I_1 = R_1^2 / R_2^2 - 6. Intensidad (
I) y Potencia (P)
(Intensidad. Unidades: W/m²)I = P / S
(Relación de intensidades y potencias, si el área de propagaciónI_1 / I_2 = P_1 / P_2Ses la misma) - 7. Efecto Doppler
(Frecuencia percibidaf_v = f_r \left(\frac{c + v}{c}\right)f_ven el efecto Doppler, para observador acercándose a fuente estacionaria.f_res la frecuencia de la fuente,cla velocidad de la onda en el medio,vla velocidad del observador. Unidades: m/s para velocidades, Hz para frecuencias) - 8. Distancia Mínima (
d_{mín})
(Distancia mínima. Unidades: m)d_{mín} = \lambda / 2 - 9. Refracción de Ondas
Si la velocidad de la onda aumenta al cambiar de medio (v_2 > v_1):- La frecuencia no varía (es constante).
- La longitud de onda aumenta (
\lambda_2 > \lambda_1). - La dirección del rayo se aleja de la normal.
- 10. Superposición de Ondas
y_T(x,t) = A \sin(\omega t - kx_1) + A \sin(\omega t - kx_2)
(Principio de superposición. Útil si se buscay_T = y_1 + y_2y_2. Unidades: m)
Armónicos (Nodos y Vientres)
Fórmulas para ondas estacionarias en diferentes configuraciones:
1. Cuerda con ambos extremos fijos (Nodo-Nodo)
- Longitud de onda (
\lambda):\lambda = (2L) / n_{armónico}(Unidades: m) - Frecuencia (
f):f = (n_{armónico} v) / (2L)(Unidades: Hz)
2. Tubo abierto en ambos extremos (Vientre-Vientre)
- Longitud de onda (
\lambda):\lambda = (2L) / n_{armónico}(Unidades: m) - Frecuencia (
f):f = (n_{armónico} v) / (2L)(Unidades: Hz)
3. Tubo cerrado en un extremo (Vientre-Nodo)
- Longitud de onda (
\lambda):\lambda = (4L) / n_{armónico}(Unidades: m) - Frecuencia (
f):f = (n_{armónico} v) / (4L)(Unidades: Hz)
Más Fórmulas de Ondas (Movimiento Armónico Simple)
- 1. Velocidad en MAS (
v)
(Unidades: m/s)v = \omega \sqrt{A^2 - x^2} - 2. Aceleración en MAS (
a)
(Unidades: m/s²)a = -\omega^2 x - 3. Energía Mecánica en MAS (
E_m)
(E_m = E_c + E_p = \frac{1}{2} k A^2kes la constante elástica del sistema. Unidades: J) - 4. Relación entre Constante Elástica, Frecuencia Angular y Masa
(Unidades: N/m)k = \omega^2 m - 5. Periodo de un Péndulo Simple (
T)
(Unidades: s)T = 2\pi \sqrt{L / g} - 6. Ecuación General de una Onda Armónica
(y(x,t) = A \sin(\omega t \pm kx)A: amplitud,\omega: frecuencia angular,k: número de onda) - 7. Intensidad de una Onda Esférica (
I)
(Útil si se busca el radioI = P / S = P / (4\pi r^2)r. Unidades: W/m²)
Campo Magnético
- 1. Campo Magnético de Hilos Rectos Paralelos
(Campo magnético resultante de dos hilos rectos paralelos.B_{total} = B_1 + B_2 = \frac{\mu_0 I_1}{2\pi d_1} + \frac{\mu_0 I_2}{2\pi d_2}\mu_0es la permeabilidad magnética del vacío. Unidades: T) - 2. Campo Magnético para N Hilos Rectos Paralelos
(Campo magnético para N hilos rectos paralelos idénticos. Unidades: T)B_{N_espiras} = N \frac{\mu_0 I}{2\pi d} - 3. Fuerza de Lorentz sobre una Carga en Movimiento (
F)
(Módulo de la fuerza de Lorentz sobre una cargaF = q v B \sin\thetaqmoviéndose con velocidadven un campo magnéticoB.\thetaes el ángulo entre\vec{v}y\vec{B}. Unidades: N) - 4. Campo Magnético en el Centro de una Espira Circular (
B)
(Campo magnético en el centro de una espira circular de radioB = \frac{\mu_0 I}{2R}Rcon corrienteI. Unidades: T)
Óptica Ondulatoria y Geométrica
- 1. Índice de Refracción (
n)
(n = c / v_{medio}ces la velocidad de la luz en el vacío,v_{medio}es la velocidad de la luz en el medio) - 2. Ley de Snell (Refracción)
(Para calcular el ángulo de refracciónn_1 \sin i = n_2 \sin rr) - 3. Reflexión Total Interna
Condición: El ángulo de refracción esr = 90°. - 4. Relación entre Ángulos, Velocidades e Índices de Refracción
(Útil para calcular la velocidad de la luz en el segundo medio\frac{\sin i}{\sin r} = \frac{v_1}{v_2} = \frac{n_2}{n_1}v_2)
Espejos y Lentes
Espejos
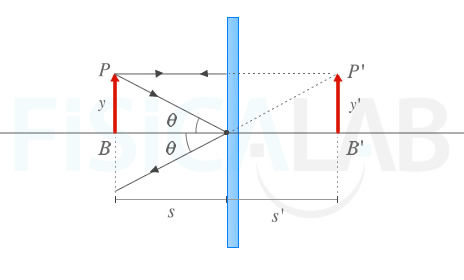 Espejo Plano
Espejo Plano
Características de la imagen: mismo tamaño, derecha, virtual.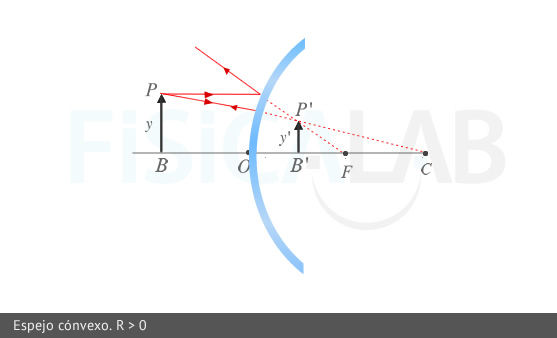 Espejo Convexo
Espejo Convexo
Características de la imagen: más pequeña, derecha, virtual.- Espejo Cóncavo
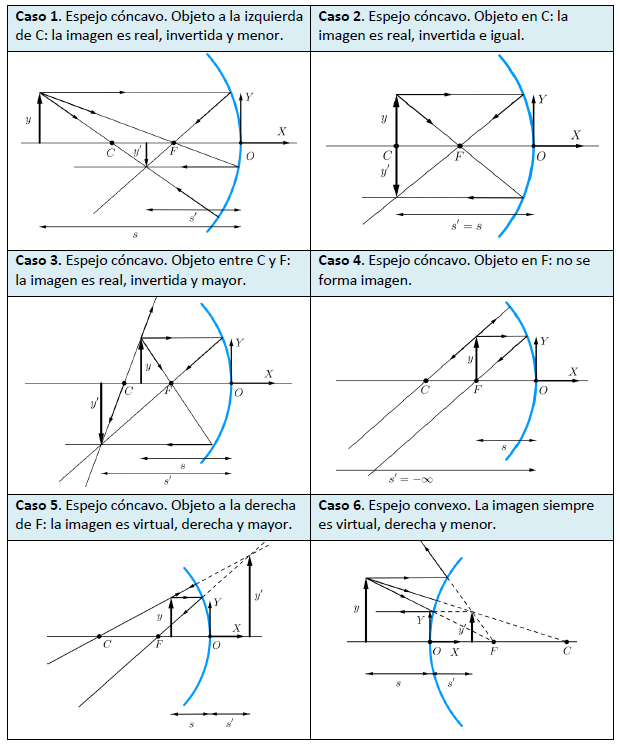
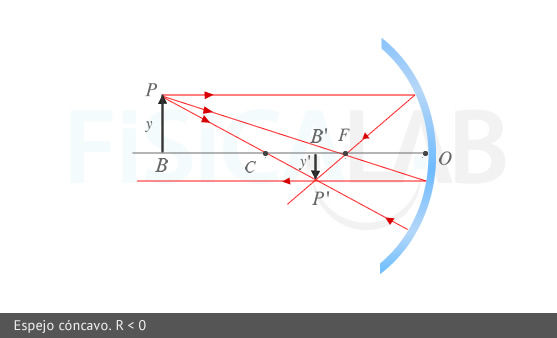 Objeto entre (-∞) y el centro de curvatura (C): Imagen más pequeña, invertida, real.
Objeto entre (-∞) y el centro de curvatura (C): Imagen más pequeña, invertida, real. Objeto entre el foco (F) y el centro de curvatura (C): Imagen más grande, invertida, real.
Objeto entre el foco (F) y el centro de curvatura (C): Imagen más grande, invertida, real. Objeto en el centro de curvatura (C): Imagen del mismo tamaño, invertida, real.
Objeto en el centro de curvatura (C): Imagen del mismo tamaño, invertida, real. Objeto en el foco (F): No se forma imagen (los rayos son paralelos).
Objeto en el foco (F): No se forma imagen (los rayos son paralelos). Objeto entre el foco (F) y el vértice (V) del espejo: Imagen más grande, derecha, virtual.
Objeto entre el foco (F) y el vértice (V) del espejo: Imagen más grande, derecha, virtual.
Fórmulas de Espejos
Aumento Lateral (M)
M = y' / y = -s' / s
Donde:
y: tamaño del objetoy': tamaño de la imagens: distancia del objeto al espejos': distancia de la imagen al espejo
Ecuación del Fabricante de Espejos
1/f = 1/s + 1/s'
s' + s = d (Relación de distancias, específica para ciertos sistemas ópticos)
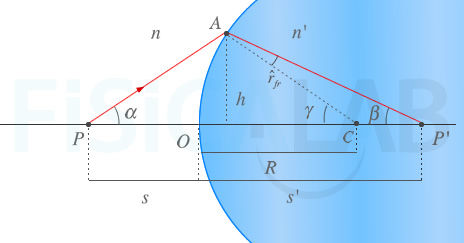
Dioptrio Esférico
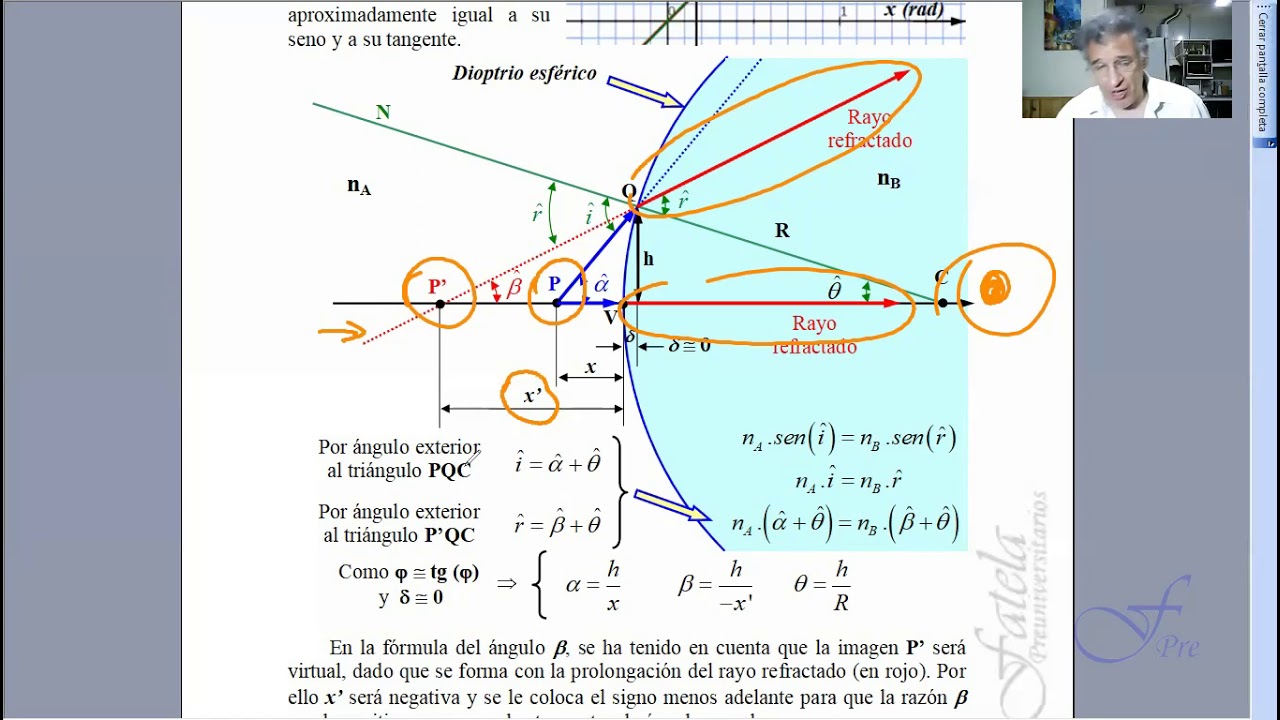
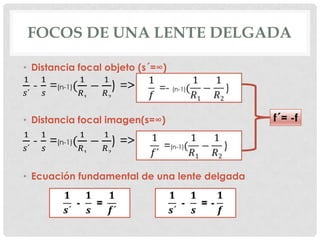
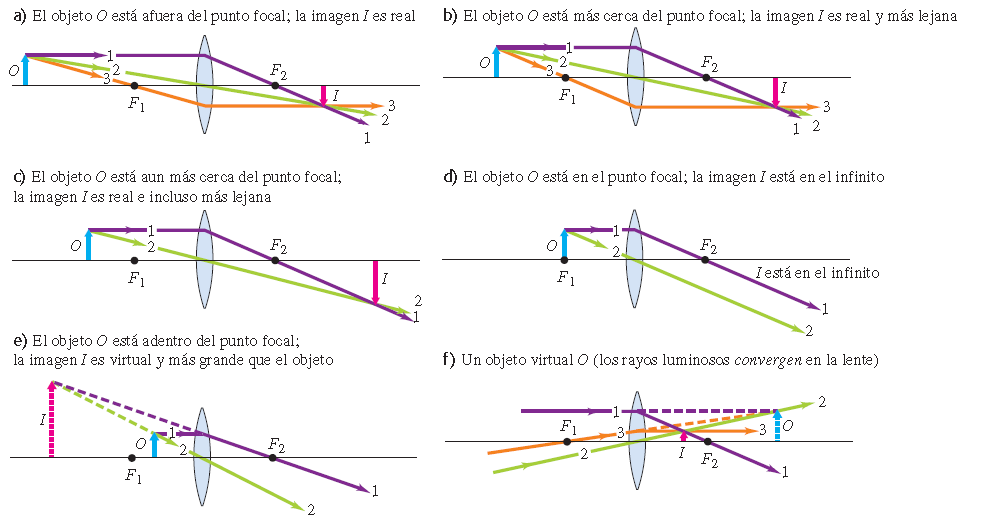
Lentes