Producto escalar

Enviado por Javi y clasificado en Matemáticas

Escrito el 28 de Noviembre de 2007 en español con un tamaño de 2,55 KB

El producto escalar en el caso particular de dos vectores en el plano,o en un espacio euclídeo N-dimensional, se define como el producto desus módulos multiplicado por el coseno del ángulo $?$ que forman. El resultado es siempre una magnitud escalar. Se representapor un punto, para distinguirlo del producto vectorial que serepresenta por un aspa: $\\\\\\\\\\\\\\\\vec{A} \\\\\\\\\\\\\\\\cdot \\\\\\\\\\\\\\\\vec{B}=|\\\\\\\\\\\\\\\\vec{A}| |\\\\\\\\\\\\\\\\vec{B}| cos \\\\\\\\\\\\\\\\theta$

El producto escalar también puede calcularse a partir de lascoordenadas cartesianas de ambos vectores, en una baseortonormal(ortogonal y unitaria, es decir, con vectores de tamaño igual a launidad y que forman ángulos rectos entre sí):

$\\\\\\\\\\\\\\\\vec{A}\\\\\\\\\\\\\\\\cdot\\\\\\\\\\\\\\\\vec{B}=(a_1, a_2, a_3)\\\\\\\\\\\\\\\\cdot(b_1,b_2,b_3)=a_1 b_1 + a_2 b_2 + a_3 b_3$

Propiedades del producto escalar en un espacio euclídeo real[editar]

Conmutativa:

$\\\\\\\\\\\\\\\\vec{A} \\\\\\\\\\\\\\\\cdot \\\\\\\\\\\\\\\\vec{B}=\\\\\\\\\\\\\\\\vec{B} \\\\\\\\\\\\\\\\cdot \\\\\\\\\\\\\\\\vec{A}$

Asociativa:

$m (\\\\\\\\\\\\\\\\vec{A} \\\\\\\\\\\\\\\\cdot \\\\\\\\\\\\\\\\vec{B})= (m\\\\\\\\\\\\\\\\vec{A}) \\\\\\\\\\\\\\\\cdot \\\\\\\\\\\\\\\\vec{B}=\\\\\\\\\\\\\\\\vec{A}\\\\\\\\\\\\\\\\cdot(m\\\\\\\\\\\\\\\\vec{B})$ siendo m un escalar.

Distributiva:

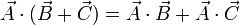
$\\\\\\\\\\\\\\\\vec{A}\\\\\\\\\\\\\\\\cdot(\\\\\\\\\\\\\\\\vec{B}+\\\\\\\\\\\\\\\\vec{C})=\\\\\\\\\\\\\\\\vec{A}\\\\\\\\\\\\\\\\cdot\\\\\\\\\\\\\\\\vec{B}+\\\\\\\\\\\\\\\\vec{A}\\\\\\\\\\\\\\\\cdot\\\\\\\\\\\\\\\\vec{C}$

Si los vectores son ortogonales, su producto escalar es nulo (cos 90º = 0).

Entradas relacionadas:

Etiquetas: