Aceleración

Enviado por Javi y clasificado en Física

Escrito el 25 de Octubre de 2007 en español con un tamaño de 8,12 KB

La aceleración es la magnitud física que mide la tasa de variación de la velocidad respecto del tiempo. Es una magnitud vectorial con dimensiones de longitud/tiempo² (en unidades del sistema internacional se usa generalmente [m/s²]). No debe confundirse la celeridad con la aceleración, pues son conceptos distintos, acelerar no significa ir más rápido, sino cambiar de velocidad a un ritmo dado.

Aceleración media e instantánea

Aceleración instantánea es representada como la pendiente de la recta tangente de la curva de representación velocidad-tiempo.

Se define la aceleración media como la relación entre la variación o cambio de velocidad de un móvil y el tiempo empleado en dicho cambio de velocidad:

$a= \\\\frac{v-v_0}{t-t_0} = \\\\frac{\\\\Delta v}{\\\\Delta t}$

Donde a es aceleración, y v la velocidad final en el instante t, $v 0$ la velocidad inicial en el instante t₀.

La aceleración instantánea, que para trayectorias curvas se toma como un vector, es la derivada de la velocidad (instantánea) respecto del tiempo en un instante dado (en dos instantes cercanos pero diferentes el valor puede cambiar mucho):

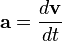$\\\\mathbf{a}=\\\\frac{d\\\\mathbf{v}}{dt}$

Puesto que la velocidad instantánea v a su vez es la derivada del vector de posición r respecto al tiempo, se tiene que la aceleración vectorial es la derivada segunda respecto de la variable temporal:

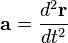$\\\\mathbf{a} = \\\\frac{d^2 \\\\mathbf{r}}{dt^2}$

De igual forma se puede definir la velocidad instantánea a partir de la acelaración como

$v=\\\\int_0^n \\\\left({\\\\mathrm{d}v \\\\over \\\\mathrm{d}t}\\\\right)\\\\,\\\\mathrm{d}t$

O incluso también, la velocidad puede entenderse como la integral de la aceleración respecto el tiempo, es de notar que la integración puede ser definda o indefinida:

$v=\\\\int_0^n a\\\\,\\\\mathrm{d}t$ ,

Componentes intrínsecas de la aceleración: aceleraciones tangencial y normal

Existe una descomposición geométrica útil del vector de aceleración de una partícula, en dos componentes perpendiculares: la aceleración tangencial y la aceleración normal. La primera da cuenta de cuanto varía el módulo del vector velocidad o celeridad. La aceleración normal por el contrario da cuenta de la tasa de cambio de la dirección velocidad:

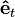$\\\\mathbf{a}= \\\\frac{d\\\\mathbf{v}}{dt} = \\\\frac{d}{dt}(\\\\left \\\\Vert \\\\mathbf{v} \\\\right \\\\|\\\\mathbf{\\\\hat{e}}_t) = \\\\frac{d\\\\left \\\\Vert \\\\mathbf{v} \\\\right \\\\|}{dt}\\\\mathbf{\\\\hat{e}}_t + \\\\left \\\\Vert \\\\mathbf{v} \\\\right \\\\|\\\\frac{d\\\\mathbf{\\\\hat{e}}_t}{dt} = a_t \\\\mathbf{\\\\hat{e}}_t + \\\\left \\\\Vert \\\\mathbf{v} \\\\right \\\\| (\\\\boldsymbol{\\\\omega} \\\\times \\\\hat{e}_t)$

Donde $\\\\mathbf{\\\\hat{e}}_t$ es el vector unitario y tangente a la trayectoria del mismo sentido que la velocidad. Usando las fórmulas de geometría diferencial de curvas se llega a que la expresión anterior es igual a:

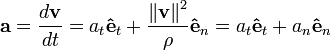
$\\\\mathbf{a}= \\\\frac{d\\\\mathbf{v}}{dt} = a_t \\\\mathbf{\\\\hat{e}}_t + \\\\frac{\\\\left \\\\Vert \\\\mathbf{v} \\\\right \\\\|^2}{\\\\rho} \\\\mathbf{\\\\hat{e}}_n = a_t \\\\mathbf{\\\\hat{e}}_t + a_n \\\\mathbf{\\\\hat{e}}_n$

Donde a_t es la aceleración tangencial, a_n es la aceleración normal y los vectores que aparecen en la anterior expresión se relacionan con los vectores del triedro de Frênet que aparece en la geometría diferencial de curvas del siguiente modo:

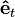$\\\\mathbf{\\\\hat{e}}_t$ es el vector unitario tangente a la curva. $\\\\mathbf{\\\\hat{e}}_n$ es el vector normal (unitario) de la curva. $\\\\boldsymbol{\\\\omega}$ es el vector velocidad angular que es siempre paralelo al vector binormal de la curva.

Movimiento Circular uniforme

Un movimiento circular uniforme es aquél en el que la partícula recorre una trayectoria circular de radio R con celeridad constante, es decir, que la distancia recorrida en cada intervalo de tiempo igual es la misma. Para ese tipo de movimiento el vector de velocidad aunque mantiene su módulo va variando ligeramente la dirección para completar el círculo al cabo de un ciclo. Si se aplican las fórmulas anteriores, se tiene que la aceleración tangencial se anula y la aceleración normal es constante, por lo que en un movimiento circular uniforme la aceleración es constante en módulo y siempre es perpendicular a la velocidad:

$\\\\mathbf{a}= \\\\frac{d\\\\mathbf{v}}{dt} = \\\\frac{d\\\\left \\\\Vert \\\\mathbf{v} \\\\right \\\\|}{dt}\\\\mathbf{\\\\hat{e}}_t + \\\\frac{\\\\left \\\\Vert \\\\mathbf{v} \\\\right \\\\|^2}{R} \\\\mathbf{\\\\hat{e}}_n = 0 \\\\cdot \\\\mathbf{\\\\hat{e}}_t + \\\\frac{v^2}{r} \\\\hat{\\\\mathbf{e}}_n = - \\\\omega^2 \\\\mathbf{r}$

Unidades

A parte de emplear las unidades de tiempo: longitud/tiempo² (en unidades del sistema internacional se usa generalmente [m/s²]. Además es muy común en los ámbitos aeronáuticos emplear g, un g (más específicamente, g_n o g ₀) es la aceleración standard de caída libre de los cuerpos cuyo valor es 9.80665 m/s², causada por el campo gravitatorio de la Tierra al nivel del mar a una latitud de 45.5°.

Entradas relacionadas:

Etiquetas:

formula de aceleracion fisica aceleracion aceleracion concepto de aceleracion en fisica significado de aceleracion en fisica aceleracion formula fisica aceleracion media aceleracion media e instantanea aceleracion instantanea formula integral de la aceleracion aceleracion fisica como se halla la aceleracion concepto de aceleracion media aceleracion instantanea definicion aceleracion media definicion aceleración instantánea aceleracion media formula aceleracion media fisica formula de aceleracion instantanea formula aceleración media que es aceleracion en fisica velocidad instantanea aceleracion definicion fisica definicion de aceleracion media aceleracion media definicion y formula formulas de fisica aceleracion que es aceleracion formula de aceleracion en fisica aceleracion formula definicion de aceleracion en fisica