Operaciones con vectores

Enviado por Javi y clasificado en Matemáticas

Escrito el 28 de Noviembre de 2007 en español con un tamaño de 9,9 KB

Suma de vectores

Gráficamente, se pueden sumar vectores por dos metodos: el delparalelogramo y el del polígono. El del paralelogramo basicamenteconsiste en reproducir los dos vectores, contrariamente, es decir, sihay un vector llamado "a" y otro llamado "b", en el metodo delparalelogramo, la reproduccion de "b" estaria al finalizar "a" yviceversa, formando un paralelogramo. El resultado se sacaria uniendodel punto central hacia donde se juntan las reproducciones de "a" y "b"El método del triángulo se parece al metodo del poligono, a diferenciade que el metodo del triangulo solo se admiten 2 vectores y en el delpolígono son más de dos El método del triángulo consiste en hacer unacontinuación a partir de otro, es decir, tenemos vector "a" y vector"b" donde termina vector v se inicia el vector z y para la resultantesolo se une de un punto de inicio hacia donde termina.

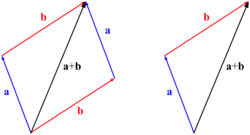
Partiendo de la representación gráfica de dos vectores, la suma deambos se consigue colocando el punto de aplicación del segundo vector,a continuación de la flecha del primero, el vector resultante es el queparte del punto de aplicación del primero hasta el final de la flechadel segundo.

Analíticamente, partiendo de las coordenadas de los dos vectores:

$\\\\\\\\\\\\\\\\vec{a} = (a_x, a_y, a_z)$ $\\\\\\\\\\\\\\\\vec{b} = (b_x, b_y, b_z)$

El vector suma será:

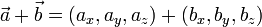
$\\\\\\\\\\\\\\\\vec{a} + \\\\\\\\\\\\\\\\vec{b} = (a_x, a_y, a_z) + (b_x, b_y, b_z)$

agrupando:

$\\\\\\\\\\\\\\\\vec{a} + \\\\\\\\\\\\\\\\vec{b} = (a_x+b_x,a_y+b_y,a_z+b_z)$

Representando los vectores como combinación lineal de vectores tenemos:

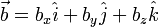
$\\\\\\\\\\\\\\\\vec{a} = a_x \\\\\\\\\\\\\\\\hat{i} + a_y \\\\\\\\\\\\\\\\hat{j} + a_z \\\\\\\\\\\\\\\\hat{k}$ $\\\\\\\\\\\\\\\\vec{b} = b_x \\\\\\\\\\\\\\\\hat{i} + b_y \\\\\\\\\\\\\\\\hat{j} + b_z \\\\\\\\\\\\\\\\hat{k}$

El resultado de la suma es:

$\\\\\\\\\\\\\\\\vec{a}+ \\\\\\\\\\\\\\\\vec{b} = (a_x \\\\\\\\\\\\\\\\hat{i} + a_y \\\\\\\\\\\\\\\\hat{j} + a_z \\\\\\\\\\\\\\\\hat{k}) + (b_x \\\\\\\\\\\\\\\\hat{i} + b_y \\\\\\\\\\\\\\\\hat{j} + b_z \\\\\\\\\\\\\\\\hat{k})$

ordenando los componentes:

$\\\\\\\\\\\\\\\\vec{a}+ \\\\\\\\\\\\\\\\vec{b} = (a_x + b_x) \\\\\\\\\\\\\\\\hat{i} + (a_y + b_y) \\\\\\\\\\\\\\\\hat{j} + (a_z + b_z) \\\\\\\\\\\\\\\\hat{k}$

Pongamos un ejemplo numérico:

$\\\\\\\\\\\\\\\\vec{a} = 3 \\\\\\\\\\\\\\\\hat{i} + 5 \\\\\\\\\\\\\\\\hat{j} - 4 \\\\\\\\\\\\\\\\hat{k}$ $\\\\\\\\\\\\\\\\vec{b} = -4 \\\\\\\\\\\\\\\\hat{i} + 6 \\\\\\\\\\\\\\\\hat{j} -2 \\\\\\\\\\\\\\\\hat{k}$

el resultado:

$\\\\\\\\\\\\\\\\vec{a}+ \\\\\\\\\\\\\\\\vec{b} = (3 \\\\\\\\\\\\\\\\hat{i} + 5 \\\\\\\\\\\\\\\\hat{j} - 4 \\\\\\\\\\\\\\\\hat{k}) + (-4 \\\\\\\\\\\\\\\\hat{i} + 6 \\\\\\\\\\\\\\\\hat{j} -2 \\\\\\\\\\\\\\\\hat{k})$

agrupando términos:

$\\\\\\\\\\\\\\\\vec{a}+ \\\\\\\\\\\\\\\\vec{b} = (3 - 4) \\\\\\\\\\\\\\\\hat{i} + (5 + 6) \\\\\\\\\\\\\\\\hat{j} + (-4 - 2) \\\\\\\\\\\\\\\\hat{k}$

esto es:

$\\\\\\\\\\\\\\\\vec{a}+ \\\\\\\\\\\\\\\\vec{b} = - \\\\\\\\\\\\\\\\hat{i} + 11 \\\\\\\\\\\\\\\\hat{j} - 6 \\\\\\\\\\\\\\\\hat{k}$

Resta de vectores

La resta de dos vectores es la suma del primero con el opuesto del segundo.

Para hacer la diferencia de dos vectores, basta con aplicar A - B = A + (-B), esto es, sumar el vector opuesto.

Producto por un escalar

Multiplicar un vector por un escalar es tomar el vector tantas vecescomo indique el escalar, esto es valido también en los casos en los queel escalar es fraccionario o negativo.

Si partimos de la representación gráfica del vector, y sobre lamisma línea de su dirección tomamos tantas veces el módulo de vectorcomo marque el escalar, el resultado es el producto del vector por esteescalar, si el signo del escalar es negativo, es sentido del vectorserá el opuesto al original.

Partiendo de un escalar $n \\\\\\\\\\\\\\\\,$ y de un vector $\\\\\\\\\\\\\\\\vec{a}$ , el producto de $n \\\\\\\\\\\\\\\\,$ por $\\\\\\\\\\\\\\\\vec{a}$ es $n \\\\\\\\\\\\\\\\, \\\\\\\\\\\\\\\\vec{a}$ , es el producto de cada una de las coordenadas del vector por el escalar, representando el vector por sus coordenadas:

$\\\\\\\\\\\\\\\\vec{a} = (a_x, a_y, a_z)$

si lo multiplicamos por el escalar n:

$n \\\\\\\\\\\\\\\\cdot \\\\\\\\\\\\\\\\vec{a} = n \\\\\\\\\\\\\\\\cdot (a_x, a_y, a_z)$

esto es:

$n \\\\\\\\\\\\\\\\cdot \\\\\\\\\\\\\\\\vec{a} = (n \\\\\\\\\\\\\\\\cdot a_x, n \\\\\\\\\\\\\\\\cdot a_y, n \\\\\\\\\\\\\\\\cdot a_z)$

Representando el vector como combinación lineal de los versores:

$\\\\\\\\\\\\\\\\vec{a} = a_x \\\\\\\\\\\\\\\\hat{i} + a_y \\\\\\\\\\\\\\\\hat{j} + a_z \\\\\\\\\\\\\\\\hat{k}$

y multiplicándolo por un escalar n:

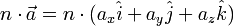
$n \\\\\\\\\\\\\\\\cdot \\\\\\\\\\\\\\\\vec{a} = n \\\\\\\\\\\\\\\\cdot (a_x \\\\\\\\\\\\\\\\hat{i} + a_y \\\\\\\\\\\\\\\\hat{j} + a_z \\\\\\\\\\\\\\\\hat{k})$

esto es:

$n \\\\\\\\\\\\\\\\cdot \\\\\\\\\\\\\\\\vec{a} = n \\\\\\\\\\\\\\\\cdot a_x \\\\\\\\\\\\\\\\hat{i} + n \\\\\\\\\\\\\\\\cdot a_y \\\\\\\\\\\\\\\\hat{j} + n \\\\\\\\\\\\\\\\cdot a_z \\\\\\\\\\\\\\\\hat{k}$

Hagamos un ejemplo con valores numéricos, partimos del vector:

$\\\\\\\\\\\\\\\\vec{a} = 3,2 \\\\\\\\\\\\\\\\hat{i} - 1,27 \\\\\\\\\\\\\\\\hat{j} + 6 \\\\\\\\\\\\\\\\hat{k}$

y multiplicamos el vector por 2,5:

$2,5 \\\\\\\\\\\\\\\\cdot \\\\\\\\\\\\\\\\vec{a} = 2,5 \\\\\\\\\\\\\\\\cdot (3,2 \\\\\\\\\\\\\\\\hat{i} - 1,27 \\\\\\\\\\\\\\\\hat{j} + 6 \\\\\\\\\\\\\\\\hat{k})$

esto es:

$2,5 \\\\\\\\\\\\\\\\cdot \\\\\\\\\\\\\\\\vec{a} = 2,5 \\\\\\\\\\\\\\\\cdot 3,2 \\\\\\\\\\\\\\\\hat{i} + 2,5 \\\\\\\\\\\\\\\\cdot (- 1,27) \\\\\\\\\\\\\\\\hat{j} + 2,5 \\\\\\\\\\\\\\\\cdot 6 \\\\\\\\\\\\\\\\hat{k}$

haciendo las operaciones:

$2,5 \\\\\\\\\\\\\\\\cdot \\\\\\\\\\\\\\\\vec{a} = 8 \\\\\\\\\\\\\\\\hat{i} - 3,175 \\\\\\\\\\\\\\\\hat{j} + 15 \\\\\\\\\\\\\\\\hat{k}$

Entradas relacionadas:

Etiquetas: