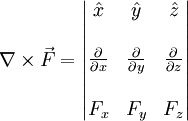Circulación y rotacional de un vector. Teorema de Stokes

Enviado por Programa Chuletas y clasificado en Física

Escrito el 20 de Junio de 2008 en español con un tamaño de 2,67 KB

6.CIRCULACIÓN DE UN VECTOR
Se define circulación de un vector a lo largo de una línea al producto escalar del vector por el vector representativo de dicha línea

7.ROTACIONAL
Dado un campo vectorial , se denimina rotacional de a una aplicación vectorial q.en cada punto P del campo le hace corresponder otro vector tal que,definida una superficie q.contenga a P, la dirección de dicho vector es normal a la superficie,su módulo corresponde a la circulación de a lo largo de la línea q.limita dicha superficie, y su sentido corresponde al avance de un tornillo q. gire en el sentido en el q.la circulación se calcula:

$\\nabla\\times \\vec F =\\left( \\frac{\\partial F_z}{\\partial y} - \\frac{\\partial F_y}{\\partial z}\\right)\\hat x + \\left(\\frac{\\partial F_x}{\\partial z} - \\frac{\\partial F_z}{\\partial x}\\right)\\hat y + \\left(\\frac{\\partial F_y}{\\partial x} - \\frac{\\partial F_x}{\\partial y}\\right)\\hat z$

O mediante el operador Nabla:

$\\nabla\\times \\vec F=\\left| \\begin{matrix} \\hat x & \\hat y & \\hat z \\\\ & & \\\\ \\frac{\\partial}{\\partial x} & \\frac{\\partial}{\\partial y} & \\frac{\\partial}{\\partial z} \\\\ & & \\\\ F_x & F_y & F_z \\end{matrix}\\right|$

8.TEOREMA DE STOKES Ó DEL ROTACIONAL
La circulación de un vector a lo largo de una línea cerrada es iugal al flujo del rotacional de dicho vector calculado sobre una superficie q.tiene esa línea como borde.Relaciona la circulación con el rotacional

Entradas relacionadas: